Giải bài 1, 2, 3, 4, 5 trang 107, 108 Sách giáo khoa Toán 7

Bài 1 Trang 107 – SGK Toán 7 Tập 1

Bạn Đang Xem: Giải bài 1, 2, 3, 4, 5 trang 107, 108 Sách giáo khoa Toán 7

Tính toán số đo \(x\) và \(y\) trong biểu đồ 47,48.49,50,51:

Người chiến thắng:

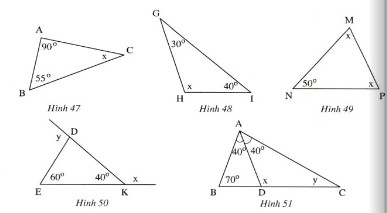
Hình 47)

Theo tổng ba góc trong trong định lý tam giác, ta có: \(x + {{90}^0} + {{55}^{0}} = {{180}^0} \) (\rightarrow x = {{180}^0} – \left( {{{90}^0} + {{55}^0}} \right) = {{35}^ 0} )

Nhô ra 48)

Theo tổng ba góc trong của tam giác, ta có:

\(x + {\rm{ }}{{40}^0} + {\rm{ }}{{30}^0} = {\rm{ }}{{180}^ 0}\)\(= > {\rm{ }}x = {\rm{ }}{{180}^0}{\rm{ – }}\left( {{\ ) rm{ }}{{40}^0} + {\rm{ }}{{30}^0}} \right) = {\rm{ }}{{110}^0}\)

Nhô ra 49)

Theo tổng ba góc trong của tam giác, ta có:

\(x + {\rm{ }}x + {\rm{ }}{{50}^0} = 180^0\)\( \rightarrow {\rm{ } }2x = {\rm{ }}{{180}^0} – {{50}^0} = {{130}^0}\)

\(x = {65}^0\)

Hình 50)

Vì \(y\) là góc ngoài của tam giác tại đỉnh \(d\) nên ta có:

\(y = {\rm{ }}{60^0} + {\rm{ }}{40^0} = {\rm{ }}{100^0}\)

Hai góc \(x\) và \(\widehat{dke}\) là hai góc kề bù nên:

\(x + {{40}^0} ={180}^{0}\)

\(x = {{180}^0} – {{40}^{0}} = 140^0\)

Xem Thêm: Những bài thơ tình buồn khiến bạn xúc động rơi nước mắt

Hình 51)

Áp dụng định lý tổng ba góc trong của tam giác cho \(\delta abc\) ta có:

\(\widehat a + \widehat b + \widehat c=180^0\)

\(({40^0} + {\rm{ }}{40^0}){\rm{ }} + {\rm{ }}{70^0} + {\ rm{ }}y{\rm{ }} = {180^0}\)

\(y+ 150^0 =180^0\)

\(y = {180^{0}} – {\rm{ }}{150^0} = {\rm{ }}{30^{0}}\)

Xem Thêm : Tóc tiên là món gì? Tóc tiên có ngon không?

Áp dụng định lý tổng ba góc trong của tam giác cho \(\delta acd\) ta có:

\(x + {\rm{ }}{40^0} + {\rm{ }}{30^0} = {\rm{ }}{180^0}\)

\(x = {\rm{ }}{180^0} – ({\rm{ }}{40^0} + {\rm{ 3}}{0^0}) = {\rm{ }}{110^0}\)

Bài 2 Trang 108 – SGK Toán 7

Đối với tam giác \(abc\): \(\widehat{b}= 80^0\), \(\widehat{c}= 30^0\). Tia phân giác của góc \(a\) cắt \(bc\) tại \(d\). Tính \(\widehat{adc},\widehat{adb}\).

Người chiến thắng:

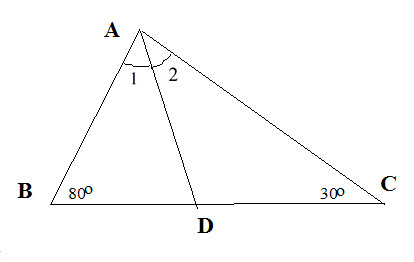
Theo tổng ba góc của tam giác ta có:

\(\widehat {bac} + \widehat b + \widehat c = {180^0}\)

\(\widehat{bac}= 180^0- (\widehat{b}+\widehat{c})\) = \(180^0-( 80^0+ 30^ 0)= 70^0\)

Bởi vì \(ad\) là \(\widehat{bac}\) \(\widehat{a_{1}}\)=\(\ widehat{ a_{2 }}\)

\(\widehat{a_{1}}\)=\(\widehat{a_{2}}\)=\(\frac{\widehat{bac}}2 \)=\(\frac{70^{0}}2= 35^0\)

\(\widehat{adc}\) = \(\widehat{b}\) + \(\widehat{a_{1}}\) (góc ngoài của tam giác )

Xem Thêm: Trọn bộ bài tập thì hiện tại hoàn thành tiếp diễn từ cơ bản đến nâng cao (có đáp án)

\(=80^0+ 35^0= 115^0\)

Hai góc \(\widehat{adc}\) và \(\widehat{adb}\) là hai góc kề bù

Do đó \(\widehat{adb}= 180^0- \widehat{adc}= 180^0-115^0=65^0\)

Bài 3 Trang 108 – SGK Toán 7

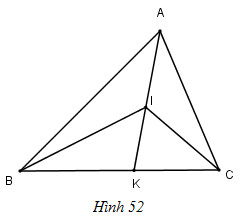
Đối với Hình 52. So sánh:

a) \(\widehat{bik}\) và \(\widehat{bak}\).

b) \(\widehat{bic}\) và \(\widehat{bac}\)

NGƯỜI CHIẾN THẮNG

a) Ta có \(\widehat{bik}\) là góc ngoài của \(\delta bai\).

Nên là \(\widehat{bik}=\widehat{bai }+\widehat{abi }> \widehat{bai }\) (1)

\(\widehat{bak}=\widehat{bai}\)

Vậy \(\widehat{bik}>\widehat{bak}\)

Xem Thêm : Trách nhiệm là gì? Biểu hiện và cách trở thành người có trách nhiệm?

b) Ta có \(\widehat{cik }\) là góc ngoài \(\delta aic\)

Nên là \(\widehat{cik }=\widehat{cai}+\widehat{ica}>\widehat{cai}\) (2)

Từ (1) và (2) ta có:

\(\widehat{bik}\) + \(\widehat{cik } > \widehat{bai }\) + \(\widehat{cai}\)

\(\rightarrow \widehat{bic} > \widehat{bac}\).

Bài 4 Trang 108 – SGK Toán 7 Tập 1

Xem Thêm: CÔ LIÊU CỦA HÀN MẶC TỬ VÀ TRẠNG THÁI TỘT ĐỈNH CỦA CẢM XÚC

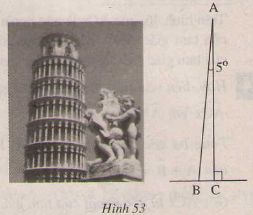
Tháp nghiêng pi – da trong tiếng Ý nghiêng \(5^0\) so với phương thẳng đứng (h.53). Tính số đo của góc \(abc\) trong hình vẽ.

Người chiến thắng:

Ta có tam giác vuông \(abc\) tại \(c\) nên

\(\widehat{a}\)+ \(\widehat{b}= 90^0\) (vì hai góc nhọn của tam giác vuông bù nhau)

Hoặc \(5^0\)+\(\widehat{b}\) = \(90^0\) \(\rightarrow {90^0} – {5 ^0} = {85^0}\)

Bài 5 Trang 108 – SGK Toán 7 Tập 1

Ta gọi tam giác có ba góc nhọn là tam giác nhọn và tam giác có một góc tù là tam giác tù. Kể tên các tam giác nhọn, tam giác tù, tam giác vuông ở hình 54.

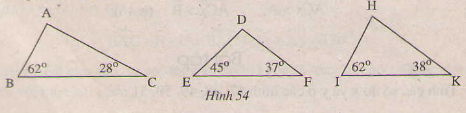
Người chiến thắng:

a) Áp dụng định lý tổng các góc trong của một tam giác vào tam giác \(abc\) ta được:

$$\eqalign{ & \widehat a + \widehat b + \widehat c = {180^0} \cr & \rightarrow \widehat a = {180^0} – \widehat b – \widehat c = {180^0} – {62^0} – {28^0} = {90^0} \cr } $$

Do đó, tam giác \(abc\) vuông góc với \(a\).

b) Áp dụng định lý tổng ba góc trong của một tam giác cho tam giác\(def\) ta được:

$$\eqalign{ & \widehat d + \widehat e + \widehat f = {180^0} \cr & \rightarrow \widehat d = {180^0} – \widehat e – \widehat f = {180^0} – {45^0} – {37^0} = {98^0} \cr } $$

Tam giác \(def\) do đó tù

c) Áp dụng Định lý Tổng tam giác cho tam giác\(hki\) ta được:

$$\eqalign{ & \widehat h + \widehat k + \widehat i = {180^0} \cr & \rightarrow \widehat h = {180^0} – \widehat k – \widehat i = {180^0} – {38^0} – {62^0} = {82^0} \cr } $$

Vậy tam giác \(hik\) nhọn.

giaibaitap.me