Khái niệm hai tam giác đồng dạng thuộc phạm vi kiến thức toán học lớp 8. Dưới đây là phần tổng hợp định nghĩa, tính chất, cách chứng minh,… có kèm theo ví dụ minh họa. Sơ đồ chi tiết và bài tập ứng dụng chi tiết về hai tam giác đồng dạng. Hãy đến và theo dõi muahangdambao.com!
Bạn Đang Xem: Thế nào là 2 tam giác đồng dạng? Tổng hợp lý thuyết và bài tập áp dụng
Thế nào là 2 tam giác đồng dạng?
Khái niệm hai tam giác đồng dạng:
*Sự đồng dạng của tam giác thường
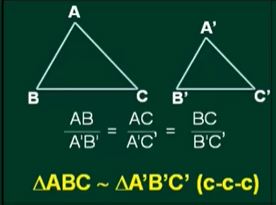
Các tam giác đồng dạng là:
- Hai tam giác có ba cặp cạnh tương ứng tỉ lệ với nhau thì bằng nhau. (bên-bên-bên).
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì bằng nhau. (góc góc).
- Hai tam giác đồng dạng nếu có hai cặp cạnh tương ứng tỉ lệ với góc giữa hai cặp cạnh đó. (cạnh góc).
- Định đề 1: Hai tam giác đồng dạng nếu cạnh huyền và góc vuông của tam giác này tỉ lệ với cạnh huyền và góc vuông của tam giác kia.
- Định đề 3: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau. (góc)
- Tỷ số của hai đường phân giác, hai đường cao, hai trung tuyến, hai đường tròn nội tiếp, bán kính ngoại tiếp và hai chu vi tương ứng của hai tam giác đồng dạng bằng nhau.
- Tỷ số diện tích của hai tam giác đồng dạng bằng bình phương tỷ số đồng dạng.
- Chứng minh hai tam giác đồng dạng
- c) có ad/cd=bd/bi; (Δadb ~ cdi )
- Chứng minh hai tam giác đồng dạng – Định lý Talet và hai đường thẳng song song
- a) adb∼△aeg
- b) ad.ae = ab.ag = ac.af
- c) fg // BC
- a) Xét abd và Δaeg, ta có:
- b) suy ra ab/ ae = ad/ ag từ a)
- c) Xét tam giác abc, ta có:
- Chứng minh hai tam giác đồng dạng—các góc tương ứng bằng nhau
- a) hbe∼△hce
- b) hed∼△hbc và góc hde = góc hae
- Cách 1:Hai tam giác được gọi là đồng dạng nếu các cạnh tương ứng và các góc tương ứng của chúng tỉ lệ với nhau.
- Phương pháp 2: Định lý Tallette: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì vẽ các đoạn thẳng tỷ lệ trên cạnh đó.
- Cách 3:cm Điều kiện cần và đủ để hai tam giác đồng dạng là: hai tam giác có độ dài các cạnh ứng với tỉ số bằng nhau. Hai tam giác có hai cặp góc tương ứng bằng nhau thì bằng nhau. Nếu hai tam giác có hai cặp cạnh tương ứng tỉ lệ và các góc giữa hai cặp cạnh đó bằng nhau thì chúng bằng nhau.
- Cách 4:Chứng minh Trường hợp 1 (cạnh nhau): Nếu 3 cạnh của tam giác này tỉ lệ với 3 cạnh của tam giác kia thì 2 tam giác đó bằng nhau.
- Cách 5: Chứng minh Trường hợp 2 (cạnh-góc-cạnh): Nếu 2 cạnh của tam giác này tỉ lệ với 2 cạnh của tam giác kia và tạo 2 góc tạo thành nếu 2 cạnh đối nhau bằng nhau thì hai tam giác đồng dạng.
- a) Chứng minh: Δbdm ∽ Δcme
- b) Chứng minh: Δmde ∽ dbm
- c) Chứng minh: bd.ce là hằng số?
- a) Ta có góc dbm = góc ecm (có trọng số Δabc tại a (1)) và góc dbm = góc dcm(gt)
- b) vì bdm cme
- c) vì bdm cme
- a) Xét tam giác abh và tam giác vuông:
- b) Xét tam giác abh có mn là trung tuyến nên mn//ab. Vậy mn ac ở k.
Ví dụ:
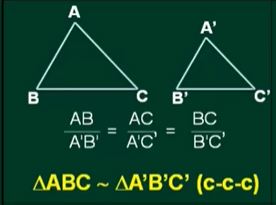
Ví dụ:
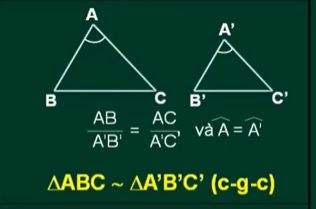
Ví dụ:
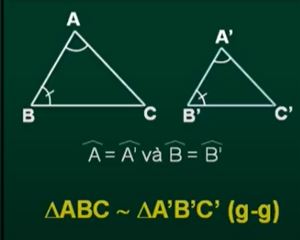
Tóm tắt sự đồng dạng của tam giác thường:
*Sự đồng dạng của tam giác vuông

Ví dụ:
Định lý 2: Hai tam giác đồng dạng nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia. (hai cạnh vuông góc)
Ví dụ:


Giả sử: △abc và △a’b’c’, với góc a = góc a’ = 90° và góc b = góc b’
Xem Thêm: Ca sĩ Lynk Lee tiết lộ lý do chuyển giới sau 30 năm ‘gồng mình’
Kết luận: ⇾△abc ~ △a’b’c’
Các tam giác đồng dạng có tính chất gì?
Từ hai tam giác đồng dạng có thể suy ra:
Cách chứng minh hai tam giác đồng dạng
Câu hỏi: Với △abc(ab<ac), ad là đường phân giác trong. Diện tích bên ngoài △ Vẽ tia cx sao cho góc bcx = góc xấu. Hãy để tôi là giao điểm của cx và ad . Bằng chứng:
a) adb∼△cdi
b) ad.ac=ab.ai
Xem Thêm : Soạn bài Số phận con người | Ngắn nhất Soạn văn 12
c) ad2 = ab.ac – bd.dc
Giải pháp: Ta có một bản vẽ:
=> ad.di = bd.cd (2) từ (1) và (2): => ab.ac – bd.cd = ad.ai – ad.di = ad(ai – di) = ad .ad = ad2
Bài toán: Cho tam giác nhọn abc, các đường cao bd, ce. Vẽ các độ cao df và eg của Δade. Bằng chứng:
Giải pháp: Hãy vẽ:
bd⊥ac (bd là đường chính)
eg⊥ac (chẳng hạn như đường cao tốc)
Suy luận: bd // Ví dụ
Suy luận: △adb∼△aeg
⇒ ad.ae = ab.ag (1)
cm tương tự, ta được: ad.ae = ac.af(2)
Suy ra từ (1) và (2):
ad.ae = ab.ag = ac.af
Xem Thêm: Văn mẫu lớp 8: Thuyết minh về di tích lịch sử Đền Hùng Dàn ý & 9 bài thuyết minh lớp 8 hay nhất
ab.ag = ac.af (cmb) suy ra: ab/af=ac/ag
Suy luận: fg // bc (định lý phản Tale)
Bài toán: Cho hai đường cao bd và ce của △abc cắt nhau tại h. Bằng chứng:
Giải pháp:Chúng tôi có hình ảnh
Góc beh = góc cdh =90∘ (gt)
Góc h1 = góc h2 (2 góc đối đỉnh)
Suy ra: hbe∼△hcd (g – g)

Phương pháp tổng hợp chứng minh hai tam giác đồng dạng môn Toán lớp 8
Bài tập Tam giác đồng dạng Toán 8
Chứng minh 2 tam giác đồng dạng.
Bài 1: Cho Δabc cân trên a; bc = 2a. Gọi m là trung điểm của bc. Lấy các điểm d, e trên ab; ac tạo góc dme=góc b
góc dbm + góc bmd + góc mdb = 180
Xem Thêm : Top 10 Bài văn phân tích bài thơ “Bác ơi!” của Tố Hữu hay nhất
dme+ bmd+cme =180०
Góc suy ra mdb= góc cme (2)
Từ (1) và (2) suy ra: Δbdm ∽ Δcme (g – g).
Vậy bd/cm=dm/tôi và bm = cm (giả sử)
bd/bm = dm/me => cơ sở dữ liệu mde.
bd/cm = bm/ce suy ra: db.ce=cm.bm
Xem Thêm: GS Nguyễn Văn Tuấn: ‘Giáo sư là chức vụ, chứ không phải phẩm hàm’
Tức là, bm=cm=bc/2= a ⇒ bd.ce = cm.bm = a2 (không đổi)
Bài tập 2: Cho ab= 12,5 cm, dc = 28,5 cm, ab//dc, góc dab = hình thang abcd của góc dbc; tính độ dài đoạn thẳng db.
Giải pháp: Hãy vẽ:
Bài 3: Cho Δabc bình phương tại a, chiều cao ah. m và n lần lượt là trung điểm của bh và ah
Bằng chứng:
a) a) có thể
b) là c
Giải pháp: Hãy vẽ:
Góc bha = góc ahc = 90
và góc bah = góc ach (cùng một phía với góc b)
⇒Δabm có thể (g.g)
⇒bh / ah = ab /ca => bm /an = ab /ca
Góc hba = góc hac (cùng một phía với góc c)
Xét abm và có thể có:
bm / an = ab/ca và góc hba = góc hac
=>Δabm có thể (c-g-c)
Xét tam giác amc, trong đó ah, mk lần lượt là các chiều cao, n là trọng tâm. Vì vậy, cn tôi
Trên đây là toàn bộ lý thuyết và hình minh họa về 2 tam giác đồng dạng và một số câu hỏi luyện tập bổ trợ về tam giác đồng dạng rất dễ hiểu khiến học sinh và phụ huynh hứng thú. Toán đặc biệt và tổng quát về hai tam giác đồng dạng của toán lớp 8. Chúc các bạn có một buổi học vui vẻ và hiệu quả.
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục