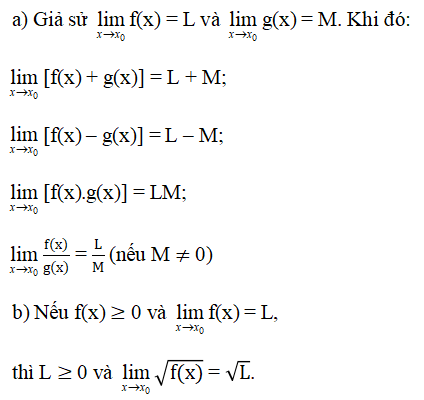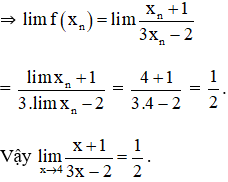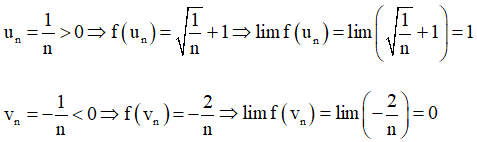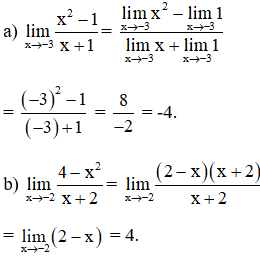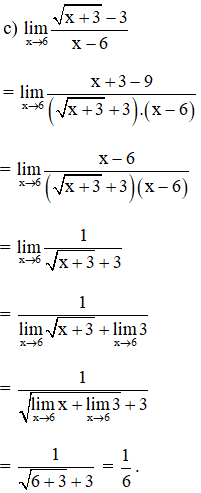Bạn Đang Xem: Giới hạn của hàm số – Giải bài tập SGK Toán 11
Trong chương trình thpt chúng ta bắt đầu học khái niệm hàm số từ lớp 10. Đến lớp 11, hàm số không chỉ dừng lại ở định nghĩa, dạng hàm và tính chất của nó, đó là những đứa trẻ. Tìm hiểu thêm về giới hạn của một hàm số và các định lý liên quan. Vậy để nắm vững kiến thức tiết học này cô và các em đến với tiết học hôm nay. Bài giảng: Giới hạn của hàm số được soạn theo chương trình sách giáo khoa, chúc mọi người có buổi học hiệu quả!
Mục tiêu khóa học
Thông qua khóa học này, bạn cần nắm vững các kiến thức sau:
- Lý thuyết giới hạn hàm số
- Giải bài tập SGK Đại số 11
- Tự luyện để thành thạo itoan.
Lý thuyết hàm giới hạn
Tổng hợp lý thuyết chi tiết & hữu ích nhất do itoan biên soạn, giúp các em có cái nhìn tổng quan và nền tảng của khóa học!
Giới hạn hữu hạn của hàm số tại một điểm
1. định nghĩa
Định nghĩa 1
Cho khoảng k chứa điểm x0 và hàm số y = f(x) xác định trên k hoặc k\{x0}.
Ta nói hàm số y = f(x) có giới hạn l khi x tiệm cận với x0, nếu với bất kỳ dãy (xn), xn ∈ k \{x0} và xn → x0, ta có f (xn ) → l.
ký hiệu: hay f(x) → l khi x → x0.
Lưu ý: trong đó c là hằng số.
2. Định lý giới hạn hữu hạn
Định lý 1
3. Hạn chế đơn phương
Xem Thêm: Giải SGK Công Nghệ 6 Bài 5: Bảo quản và chế biến thực phẩm
Định nghĩa 2
– Cho hàm số y = f(x) xác định trên (x0; b).
Khi x → x0 thì số l được gọi là giới hạn bên phải của hàm số y = f(x), nếu với mọi dãy (xn), x0 <; xn < b và xn → x0 thì ta có f(xn ) → l.
Xem Thêm: Bài 9 trang 118 Toán 6 tập 1 SGK Cánh Diều – Giải Toán lớp 6 sách
Xem Thêm : Soạn bài Bài ca ngắn đi trên bãi cát (Cao Bá Quát)
Ký hiệu:
– Cho hàm số y = f(x) xác định trên (a; x0).
Số l được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 Nếu với mọi dãy (xn), a <; xn < x0 và xn → x0 thì ta có f(xn) → l.
Xem Thêm: Bài 9 trang 118 Toán 6 tập 1 SGK Cánh Diều – Giải Toán lớp 6 sách
Xem Thêm : Soạn bài Bài ca ngắn đi trên bãi cát (Cao Bá Quát)
Ký hiệu:
Lý thuyết 2
Giới hạn hữu hạn của hàm số tại vô cực
Định nghĩa 3
a) Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn l là x → +∞ Nếu với bất kỳ dãy (xn), xn >; a và xn → +∞ thì ta có f(xn) → l.
Xem Thêm: Bài 9 trang 118 Toán 6 tập 1 SGK Cánh Diều – Giải Toán lớp 6 sách
Xem Thêm : Soạn bài Bài ca ngắn đi trên bãi cát (Cao Bá Quát)
Ký hiệu:
b) Cho hàm số y = f(x) xác định trên (-∞; a).
Ta nói hàm số y = f(x) có giới hạn l là x → -∞ Nếu với mọi dãy (xn), xn <;a và xn → -∞ thì ta có f(xn) → l.
Xem Thêm: Bài 9 trang 118 Toán 6 tập 1 SGK Cánh Diều – Giải Toán lớp 6 sách
Xem Thêm : Soạn bài Bài ca ngắn đi trên bãi cát (Cao Bá Quát)
Ký hiệu:
Lưu ý:
a) Với c, k là các hằng số và k nguyên dương, ta luôn có:
b) Định lý 1 về giới hạn hữu hạn của hàm số x → x0 vẫn đúng khi xn → +∞ hoặc x → -∞
Đáp án bài tập sgk đại số 11 giới hạn của hàm số
Bài 1 (trang 132 SGK Đại số 11):
Xem Thêm : Ý thức là gì? Nguồn gốc, bản chất và vai trò của ý thức?
Sử dụng định nghĩa để tìm các ràng buộc sau:
Giải pháp:
Nhận dãy bất kỳ (xn);xn∈d;lim xn = 4.
Xem Thêm: Công thức tính độ dài cung tròn – Bài tập chi tiết, áp dụng
b) txĐ: d = r.
Lấy bất kỳ dãy (xn) nào thỏa mãn xn → +∞
Bài 2 (trang 132 SGK Đại số 11):
Cho hàm số và dãy (un) với ; (vn) với
Tính limun, limvn, limf(un), limf(vn).
Có thể rút ra kết luận gì về giới hạn của hàm số đã cho tại x → 0?
Giải pháp:
Bài 3 (trang 132 SGK Đại số 11):
Các giới hạn sau được tính toán:
Giải pháp:
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục