Bài 11,12 ,13,14 trang 72 SGK Toán 9 tập 2 – : Liên hệ giữa cung và

1. Định lý 1

%3cp%3ev%e1%bb%9bi+hai+cung+nh%e1%bb%8f+trong+m%e1%bb%99t+%c4%91%c6%b0%e1%bb%9dng+tr%c3 %b2n+hay+hai+%c4%91%c6%b0%e1%bb%9dng+tr%c3%b2n+b%e1%ba%b1ng+nhau%3a%3c%2fp%3e

a) Hai dây cung bằng nhau thì căng dây cung bằng nhau

b) Hai dây cung bằng nhau thì vẽ hai dây cung bằng nhau

2. Định lý 2

Có hai cung ngắn trong một đường tròn hoặc hai đường tròn bằng nhau:

a) Các cung lớn hơn kéo dài các chuỗi lớn hơn

b) Sợi dây càng to thì lực căng càng lớn

Hướng dẫn giải bài tập hợp âm cung sgk trang 71,72 Toán 9 Tập 2.

Bài tập 10.a) Vẽ đường tròn tâm o bán kính r = 2 cm. Trình bày cách vẽ một cung ab 60º. Độ dài của sợi dây ab tính bằng centimet là bao nhiêu?

b) Cách chia đường tròn thành sáu cung bằng nhau như hình 12.

a) Vẽ đường tròn (o; r). Vẽ góc ở tâm 60º. Góc cắt cung là 60º (hình a).

Góc o = 60º của tam giác cân aob nên tam giác đều, suy ra ab = r.

b) Theo câu a, ta có góc ở tâm bằng dây cung ab= 60º. Kích thước của góc ở tâm được vẽ theo cách này là 360º : 60º= 6. Trên một đường tròn có thể vẽ được sáu cung bằng nhau.

Theo cái này thì cách vẽ như sau:

Vẽ 6 dây cung bằng nhau và bằng bán kính r:

Xem Thêm: Nghiên Cứu Lịch Sử

a1a2 = a2a3 = a3a4 = a4a5 ​​= a5a6 = a6a1 = r

6 cung tròn bằng nhau được suy ra từ:

cung a1a2 = a2a3 = a3a4 =a4a5= a5a6 = a6a1 = 60º (Hình b)

Xem Thêm : Giới thiệu một danh lam thắng cảnh ở quê em

Bài tập 11.Hai đường tròn bằng nhau (o) và (o’) cắt nhau tại hai điểm a và b. Vẽ các đường kính aoc, ao’d. Gọi e là giao điểm thứ hai của ac với đường tròn (o’).

a) So sánh các cung nhỏ bc, bd.

b) Chứng minh b là trung điểm của cung ebd (tức là điểm b chia cung ebd thành hai cung bằng nhau: ∩be = bd

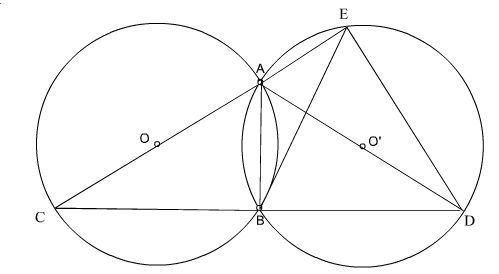
a) kết nối c với d.

Cách giải: ta có 2 hình tròn bằng nhau => ac = ad

=> ∆ cân bằng tại một

Góc abc = 90° lại vì ob = oc = oa = r (tính chất trung tuyến ứng với cạnh huyền) đồng dạng với góc abd = 90°

=>abc + abd = 180°

=> c; b; d liên tiếp, ab cd

=>bc = bd

=>cung bc = cung bd

b) nối e với d; từ b tới bh ed

Xem Thêm: Phân tích hình tượng vua Quang Trung hay nhất (13 mẫu) – Văn 9

Ta có góc dea = 90° (bằng chứng tương tự cho a)

=>bh // ec

Từ a ta có = bd

=> bh là đường trung bình của tam giác cde

=>Anh ấy=HD

Khi đó bh ⊥ ed => b là trung điểm của cung ebd

Đã xuất bản 12 trang 72. Cho tam giác abc. Lấy một điểm d trên tia đối của tia ab sao cho ad = ac. Vẽ đường tròn tâm o ngoại tiếp tam giác dbc. Các đường vuông góc hạ oh, ok từ o lần lượt là bc và bd (h ∈ bc, k ∈ bd).

a) Chứng minh ồ >OK.

b) So sánh hai cung nhỏ bd và bc.

Xem Thêm : Kết bài mở rộng là gì?

Bài 12 Trả lời:

a ) Trong tam giác abc ta có: bc <;ba + ac (bĐt) mà ac = ad (gt) ⇒ bc <;ba + ad = bd (a thuộc bd) mà: ồ ⊥ bc; được ⊥ bd (gt) ⇒ oh > ok (liên hệ chuỗi với khoảng cách từ tâm)

b) ta có bc <;bd (cmt) nên suy ra bc <;bd (nối dây cung)

Bài 13. Chứng minh rằng trong một đường tròn, hai dây cung cắt bởi hai dây cung song song thì bằng nhau.

Giải: Cho ab và cd là hai dây song song của đường tròn (o). Đường thẳng oi ⊥ ab (i ∈ ab) và ok ⊥ cd (k∈cd. do ab //cd nên i,o,k thẳng hàng. Vì tam giác oab,ocd là tam giác cân có đỉnh là o nên chiều cao Nó được vẽ. Từ đỉnh cũng là đường phân giác.

Ta có: góc ∠o1 = ∠o2, ∠o3 = ∠o4

Xem Thêm: Tính từ sở hữu trong tiếng anh: Định nghĩa, cách dùng và bài tập ứng dụng dễ hiểu

Giả sử ab là góc ngoài của cod, ta có:

∠aoc = 1800 – (∠o1 + ∠o3) = 1800 -(∠o2 + ∠o4) = ∠bod

Suy ra r arc ac= arc bd Tức là hai cung bị chắn bởi hai dây song song thì bằng nhau. Trong các trường hợp khác ta chứng minh tương tự.

Bài 14. Chứng minh rằng đường kính đi qua trung điểm của cung tròn thì đi qua trung điểm của dây cung. Mệnh đề ngược lại có đúng không? Vui lòng giải thích thêm về các điều kiện làm cho sự đảo ngược đúng. b) Chứng tỏ rằng đường kính đi qua trung điểm của cung thì vuông góc với dây cung và ngược lại.

Trả lời. a) Giả sử đường kính cd của đường tròn (o) lấy c là trung điểm của cung ab, tức là cung ac = cung cb và suy ra ∠o1 = ∠o2

Gọi i là giao điểm của cd và ab. Khi đó oi là tia phân giác của tam giác oab và cũng là đường trung tuyến (vì Δoab là đỉnh cân của tam giác o)

Vậy i là trung điểm của ab.

* Nghịch đảo không đúng vì nếu dây cung ab cũng là một đường kính thì dây cung cd đi qua trung điểm của dây cung ab chứ không đi qua trung điểm của cung ab.

* Lật lại vấn đề, ta cần nói thêm: đường kính đi qua trung điểm của một dây cung không đi qua tâm của đường tròn thì nó đi qua trung điểm của dây cung bị kéo bởi dây cung đó.

b) về phía trước: giả sử rằng đường kính cd đến c là trung điểm của cung ab ⇒ arcac = arccb

⇒ aoc = cob oc là tia phân giác của góc aob

Vì oab bằng đỉnh o nên đường phân giác cũng chính là đường cao.

Vậy: oc ab hoặc cd ab.

Đảo: Giả sử đường kính ab cd tại i.

Khi đó: oi là tia phân giác của góc ∠aob ⇒ aoc = boc ⇒ ac= bc

⇒ c là trung điểm của cung ab.