Bài tập §5. Dấu hiệu nhận biết tiếp tuyến của đường tròn Chương 2 – Đường tròn SGK Toán 9 Tập 1. Nội dung Giải bài 24 25 trang 111 112 SGK Toán 9 Tập 1 Tổng hợp các công thức, lý thuyết và phương pháp giải bài tập phần hình học trong SGK toán giúp học sinh học tốt môn Toán lớp 9.
Bạn Đang Xem: Luyện tập: Giải bài 24 25 trang 111 112 sgk Toán 9 tập 1
Lý thuyết
1. Ký hiệu nhận biết tiếp tuyến của đường tròn
Định lý: Một đường thẳng được gọi là tiếp tuyến của đường tròn nếu nó đi qua một điểm trên đường tròn và vuông góc với bán kính đi qua điểm đó.
2. Áp dụng
Bài toán: Dựng tiếp tuyến của đường tròn đi qua một điểm a nằm ngoài đường tròn $(o)$.
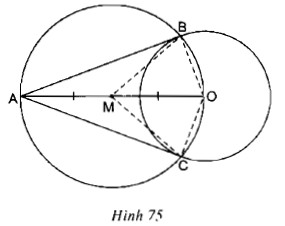
Cách xây dựng:
– Gọi $m$ là trung điểm $ao$.
– Với $m$ là tâm, $mo$ cắt $(o)$ tại $b, c.$ để tạo thành một đường tròn.
– Vẽ các đường thẳng $ab$ và $ac$. Chúng tôi nhận được tiếp tuyến mong muốn.
Dưới đây là hướng dẫn giải bài tập SGK Toán 1, tập 1, bài 24, bài 24 trang 111112 SGK Toán, các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ phần bài tập Hình học 9 và lời giải chi tiết Bài 24 trang 25 111 112 SGK Toán Tập 1 Bài 5. Để bạn tham khảo, hãy xác định các dấu hiệu của tiếp tuyến với một đường tròn trong Chương 2 – Đường tròn. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 24 trang 111 SGK Toán 9 Tập 1
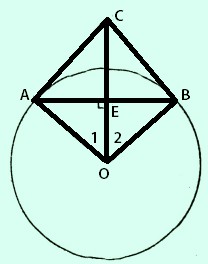
Đối với hình tròn $(o)$, đường thẳng $ab$ có đường kính khác. Vẽ một đường thẳng qua $o$ vuông góc với $ab$ cắt tiếp tuyến $a$ của đường tròn tại $c$.
a) Chứng minh rằng $cb$ là tiếp tuyến của đường tròn.
b) Cho hình tròn có bán kính $15cm, ab = 24cm$. Tính độ dài $oc$.
Giải pháp:
Xem Thêm: TOP 15 bài Phân tích 2 khổ thơ đầu bài Đây thôn Vĩ Dạ siêu hay
a) Chúng ta có $ac$ tiếp tuyến với $(o)$ nên $\widehat{oac} = 90^0 (1)$
Gọi $e$ là giao điểm của $ab$ và $oc$
$oa = ob$ (bán kính đường tròn) của tam giác $aob$
Vậy tam giác $aob$ cân tại $o$.
Chiều cao $oe$ của tam giác cân $aob$ cũng là đường phân giác. Vậy $\widehat{o_1} = \widehat{o_2}$
Xem Thêm : Bác sĩ Y-éc-xanh lớp 3 trang 107 | Giải Tiếng Việt lớp 3 Tập 2
Xét hai tam giác $aoc$ và $boc$:
$oa = ob = r$
$oc$ Chung
$\widehat{o_1} = \widehat{o_2}$
Do đó: $\delta aoc = \delta boc$
Suy ra $\widehat{oac} = \widehat{obc} (2)$
Từ (1) và (2) suy ra $\widehat{obc} = 90^0$, nghĩa là $cb \perp ob.$
Vậy $cb$ là tiếp tuyến của đường tròn $(o) (dpcm)$
b)Bán kính của hình tròn là 15, tức là $oa = 15cm$
Ta có: $oe \perp ab$
Suy ra $ea = eb = \frac{ab}{2} = \frac{24}{2} = 12$
Xem Thêm: Văn mẫu lớp 7: Cảm nghĩ về người cha thân yêu (Dàn ý 13 mẫu) Những bài văn mẫu lớp 7 hay nhất
Áp dụng định lý Pitago cho tam giác $aoe$ tại $e$, ta có:
$oe^2 = oa^2 – ae^2$
$= 15^2 – 12^2 = 225 – 144 = 81$
$⇒ oe = \sqrt{81} = 9$
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó lên cạnh huyền của tam giác vuông $aoc$, ta có:
$oa^2 = oc.oe$
$⇒ oc = \frac{oa^2}{oe} = \frac{15^2}{9} = 25$
Vậy $oc = 25 cm.$
2. Giải bài 25 trang 112 SGK Toán 9 Tập 1
Đối với đường tròn có tâm $o$ và bán kính $oa = r$, chuỗi $bc$ vuông góc với $oa$ tại trung điểm $m$ của $oa$.
a) Tứ giác $ocab$ là gì? Tại sao?
Xem Thêm : Đại danh cầm Văn Giỏi với ngón đàn triệu người mê
b) Vẽ tiếp tuyến của đường tròn tại $b$, tiếp tuyến này cắt đường thẳng $oa$ tại $e$. Tính độ dài $be$ từ $r$.
Giải pháp:
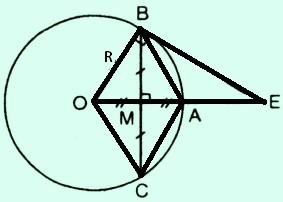
a)Chúng tôi có:
$mb = mc$ (vì $oa \perp bc$ tính bằng m)
$mo = ma$ (m là trung điểm của oa)
Xem Thêm: Soạn bài Truyện Kiều – Phần Nỗi thương mình siêu ngắn
Tứ giác $ocab$ có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành.
Mặt khác, hình bình hành $ocab$ có hai đường chéo vuông góc với nhau là $oa$ và $bc$.
Vậy tứ giác $ocab$ là hình thoi.
b)Ta có:
$ob = ba = oa = r$ (vì $ocab$ là hình thoi)
Vậy tam giác $oba$ là tam giác đều.
Suy ra $\widehat{aob} = 60^0$ hoặc $\widehat{eob} = 60^0$
Áp dụng các tỉ số lượng giác của các góc nhọn trong tam giác $obe$, ta có:
$tg \widehat{eob} = \frac{be}{ob}$
$⇒ be = ob.tg 60^0 = r\sqrt{3}$
Vậy $be = r\sqrt{3}$
Trước:
- Đáp án bài 21 22 23 trang 111 SGK toán 9 tập 1
- Giải bài 26 27 28 29 trang 115 116 SGK Toán 9 Tập 1
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học Khoa học Máy tính Lớp 9
- Học tốt GDCD lớp 9
Tiếp theo:
Xem thêm:
Chúc các em thành công trong công việc Sách Giáo Khoa Toán 9 Tập 24 Trang 25 111 112 SGK Toán 9 Tập 1!
“Môn thể thao nào đã khó giabaisgk.com”
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục





