Giải bài tập vật lý lớp 6 trang 38
Có thể bạn quan tâm
Sách giáo khoa Toán lớp 6 Trang 38, Tập 39 Tập 1 Những chân trời sáng tạo – Lời giải bài 12. ước số chung. Ước chung lớn nhất. Bài 4 trang 39: Giảm các điểm sau:
Bài 1 Trang 38 SGK Toán 6 Tập 1 – Những chân trời sáng tạo
Bạn Đang Xem: Giải bài 1, 2, 3, 4, 5 trang 38, 39 SGK Toán 6 tập 1 Chân trời sáng tạo
Trong các câu sau, câu nào đúng, câu nào sai? Trình bày sai sẽ được sửa chữa.
a) uc(12, 24) = {1; 2; 3; 4; 6; 8;12};
b) uc(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
Xem Thêm: Soạn bài Bản tin | Ngắn nhất Soạn văn 11
Phương pháp:
– Viết tập hợp các ước của a và các ước của b: u(a), u(b).
– Tìm phần tử chung của u(a) và u(b).
Giải pháp thay thế:
a) khẳng định rằng a là sai vì:
u(12) = {1; 2; 3; 4; 6; 12
u(24) = {1; 2; 3; 4; 6; 8;12; 24
Suy ra uc(12, 24) = {1; 2; 3; 4; 6; 12
Vậy 8 không phải là phần tử của tập hợp uc(12, 24).
b) Khẳng định rằng b đúng vì:
Ta có:
u(36) = {1; 2; 3; 4; 6; 9;12; 18; 36
u(12) = {1; 2; 3; 4; 6; 12
u(48) = {1; 2; 3; 4; 6; 8;12; 16; 24; 48
Suy ra uc(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
Bài 2 Trang 39 SGK Toán 6 Tập 1 – Những chân trời sáng tạo
Tìm:
a) ucln(1, 16);b) ucln(8, 20);
c) ucln(84, 156);c) ucln(16, 40, 176).
Xem Thêm: Soạn bài Bản tin | Ngắn nhất Soạn văn 11
Phương pháp:
Để tìm ucln của hai hay nhiều số lớn hơn 1, chúng ta thực hiện ba bước sau:
Bước 1: Chia mỗi số thành thừa số nguyên tố.
Bước 2: Chọn thừa số nguyên tố công khai.
Bước thứ ba: chọn tích các nhân tố, lấy chỉ số nhỏ nhất cho từng nhân tố.
Sản phẩm này là ucln cần tìm.
Giải pháp thay thế:
Xem Thêm : Soạn bài Lập dàn ý bài văn nghị luận
a) ucln(1,16) = 1.
b) 8 = 23; 20 = 22,5
=>ucln(8, 20) = 22 = 4.
c) 84 = 22.3.7;156 = 22.3.13
=>ucln(84, 156) = 22,3 = 12.
d) 16 = 24; 40 = 23,5; 176 = 24,11
=> ucln(16, 40, 176) = 23 = 8.
Bài 3 Trang 39 SGK Toán 6 Tập 1 – Những chân trời sáng tạo
a) Ta có ucln(18, 30) = 6. Viết tập hợp các ước của 6. Xét tập hợp uc(18, 30) và tập hợp a.
b) Cho hai số a và b. Để tìm tập hợp uc(a, b), ta có thể tìm tập hợp các ước của ucln(a, b). Tìm ucln, sau đó tìm tập hợp các ước chung sau:
Tôi. 24 và 30; II. 42 và 98; III. 180 và 234.
Xem Thêm: Soạn bài Bản tin | Ngắn nhất Soạn văn 11
Phương pháp:
a) Tìm bộ chia hết của 6 và nhận xét
b) Tìm tập hợp của ucln, rồi tìm tập hợp các ước của ucln.
Giải pháp thay thế:
a)Các ước của 6 là 1, 2, 3, 6.
Vậy ta có tập hợp a = u(6) = {1; 2; 3; 6}.
Xem Thêm: Top 5 Bài văn tả con vật mà em yêu thích lớp 5 hay nhất
u(18) = {1; 2; 3; 6; 9; 18}.
u(30) = {1; 2; 3; 5; 6; 10; 15; 30}.
uc(18, 30) = {1; 2; 3; 6}.
Nhận xét: Ta thấy tập uc(18, 30) = {1; 2; 3; 6} nên tập uc(18, 30) đồng dạng với tập a.
Tổng quát: Cho hai số tự nhiên a và b. Để tìm tập hợp uc(a,b), chúng ta sẽ tìm ucln(a, b) = m. Khi đó uc(a, b) = u(m).
b)
I. Giải quyết 24 và 30 là các thừa số nguyên tố: 24 = 23,3; 30 = 2,3,5.
Suy ra ucln(24, 30) = 2,3 =6.
Vậy: uc(24, 30) = u(6) = {1; 2; 3; 6}.
Hai. Ta tích hai số 42 và 98 thành thừa số nguyên tố
42 = 2,3,7;98 = 2,72
Suy ra ucln(42, 98) = 2,7 = 14.
Vậy: uc(42, 98) = u(14) = {1; 2; 7; 14}.
iii.Chúng ta phân tích các số 180 và 234 thành các số nguyên tố
180 = 22,5,32; 234 = 2,32,13
Xem Thêm : Những việc làm bảo vệ môi trường của học sinh, sinh viên
Suy ra ucln(180, 234) = 2,32 = 18
Vậy: uc(180, 234) = u(18) = {1; 2; 3; 6; 9; 18}.
Bài 4 Trang 39 SGK Toán 6 Tập 1 – Những chân trời sáng tạo
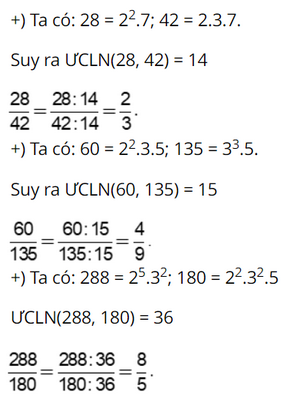
Rút gọn các phân số sau:
\(\frac{{28}}{{42}};\,\,\frac{{60}}{{135}};\,\,\frac{ {288}}{{180}}\).
Xem Thêm: Soạn bài Bản tin | Ngắn nhất Soạn văn 11
Phương pháp:
Chia cả tử số và mẫu số của phân số cho ucln của chúng.
Giải pháp thay thế:
Xem Thêm: Em hãy tả lại cảnh cổng trường giờ tan học – CungHocVui
Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho ucln của chúng để được phân số nhỏ nhất.
Bài 5 Trang 39 SGK Toán 6 Tập 1 – Những chân trời sáng tạo
Miss Blue có các dải ruy băng với ba màu khác nhau với chiều dài 140 cm, 168 cm và 210 cm. Tôi thích cắt cả ba sợi dây thành những đoạn ngắn hơn có cùng chiều dài để làm nơ trang trí mà không cần ruy băng thừa. Tính độ dài lớn nhất có thể kéo của mỗi sợi dây ngắn (độ dài của mỗi sợi dây ngắn là một số tự nhiên có đơn vị là xăng-ti-mét). Hỏi lúc đó Lan được bao nhiêu cái quai ngắn?
Xem Thêm: Soạn bài Bản tin | Ngắn nhất Soạn văn 11
Phương pháp:
Độ dài lớn nhất có thể có của mỗi xâu nhỏ cần cắt là ước chung lớn nhất của 140, 168 và 210.
Giải pháp thay thế:
Vì lan muốn cắt cả ba đoạn dây thành những đoạn ngắn hơn có cùng độ dài.
Vậy độ dài lớn nhất có thể có của mỗi đoạn dây cần cắt là ước chung lớn nhất của 140, 168 và 210.
Ta tìm ước chung lớn nhất của 140, 168, 210:
Ta có: 140 = 22,5,7
168 = 23.3.7
210 = 2.3.5.7
Suy ra ucln(140, 168, 210) = 2. 7=14.
Chiều dài tối đa có thể cắt của mỗi sợi dây ngắn: 14 cm.
-Số lượng dây có thể rút ngắn đối với mỗi dây khác nhau:
Một sợi dây dài 140 cm có thể được cắt thành: 140 : 14 = 10 (nút thắt).
Một sợi dây dài 168 cm có thể cắt thành: 168 : 14 = 12 (đoạn).
Có thể cắt một đoạn dây dài 210 cm thành: 210 : 14 = 15 (đoạn).
-Số đoạn ruy băng ngắn Lan có:
10 + 12 + 15 = 37 (chuỗi).
Kết luận: Sau khi cắt Lan được tổng cộng 37 đoạn ruy băng ngắn có chiều dài 14 cm.
sachbaitap.com
Bài viết tiếp theo
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục
