Giải bài 5, 6, 7 trang 39 SGK Hình học lớp 12 – Giaibaitap.me

bài 5 trang 39 SGK hình học lớp 12

Bạn Đang Xem: Giải bài 5, 6, 7 trang 39 SGK Hình học lớp 12 – Giaibaitap.me

Một hình trụ có bán kính đáy \(r = 5cm\) và khoảng cách đáy \(7 cm\).

a) Tính diện tích xung quanh hình trụ và thể tích của hình trụ thu được.

b) Cắt hình trụ với một mặt phẳng song song với trục một khoảng \(3 cm\). Tính diện tích phần tạo thành.

Người chiến thắng:

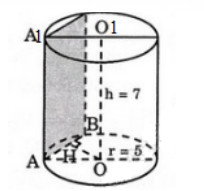
a) Theo ban đầu, chiều cao của hình trụ là \(h = 7 cm\) và bán kính đáy là \(r = 5 cm\).

Vậy diện tích xung quanh bằng:

\(s_{xq}= 2πrh = 70π\)(\(cm^2\))

Thể tích của hình trụ là:

\(v = πr^2h = 175π\) (\(cm^3\))

b) Thiết diện qua trục là hình chữ nhật có cạnh bằng chiều cao\(7 cm\) của hình trụ. Giả sử mặt cắt ngang là \(abb_1a_1\).

Xem Thêm: Testosterone là gì? Vai trò của Testosterone đối sức khỏe của nam

Ta có \(aa_1 = 7 cm, ồ= 3 cm\).

Vì tam giác \(oah\) chính xác tại \(h\) nên

\(à^2 = oa^2 – ồ^2 = 25 – 9 = 16\).

Xem Thêm : Cách vẽ tranh cổ bé bán diêm

Vậy \(ah = 4 cm, ab = 8 cm\).

Diện tích mặt cắt ngang là:

\(s=ab.aa_1=8.7=56\) (\(cm^2\)).

SGK Hình Học 12 Bài 6 Trang 39

Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được tam giác đều \(2a\). Tính diện tích và thể tích của hình nón này.

Người chiến thắng:

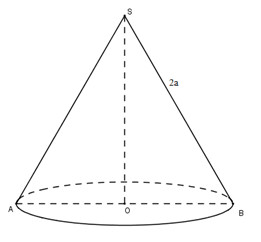
Theo đề bài thì đường kính đường tròn đáy của hình nón là \(2a\). Vậy bán kính \(r = a\).

Chiều cao của hình nón bằng chiều cao của tam giác đều nên \(h = a\sqrt3\) và đường sinh \(l = 2a\).

Xem Thêm: Mẫu bản báo cáo thu hoạch thường dùng

Vậy diện tích xung quanh hình nón là:

\(s_{xq} = πrl = 2a^2π\)

Thể tích khối nón là:

\(v = {1 \ trên 3}\pi {r^2}.h = {1 \trên 3}\pi {a^2}.a\sqrt 3 = {{ \pi {a^3}\sqrt 3 } \hơn 3}\)

SGK Hình Học 12 Bài 7 Trang 39

Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\).

a) Tính chu vi và diện tích toàn phần của hình trụ.

Xem Thêm : Luyện tập: Giải bài 20 21 22 23 24 25 trang 84 sgk Toán 9 tập 1

b) Tính thể tích khối trụ tạo bởi khối trụ đã cho.

c) Hai điểm \(a\) và \(b\) nằm trên hai đường tròn đáy tạo góc giữa đường thẳng \(ab\) và trục tọa độ bằng \( 30^0\). Tính khoảng cách giữa đường thẳng \(ab\) và trục của hình trụ

Người chiến thắng:

Theo công thức ta có:

Xem Thêm: 1 Gang Tay Dài Bao Nhiêu Cm

\(s_{xq} = 2πrh = 2\sqrt3 πr^2\)

\(s_{tp} = 2πrh + 2πr^2 = 2\sqrt3 πr^2 + 2 πr^2 \)

\(= 2(\sqrt3 + 1)πr^2\) (đơn vị âm lượng)

b) \(v\)cột = \(πr^2h = \sqrt3 π r^3\)

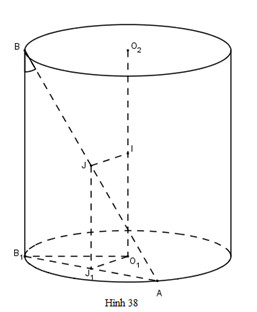
c) Giả sử trục của hình trụ là \(o_1o_2\) và \(a\) nằm trên đường tròn có tâm \(o_1\) và \(b\) nằm trên đường thẳng Tâm \(o_2\); \(i\) là trung điểm của \(o_1o_2\), \(j\) là trung điểm của \(ab\). Khi đó \(ij\) là đường vuông góc chung của \(o_1o_2\) và \(ab\). hạ \(bb_1\) vuông góc với đáy và \(j_1\) là hình chiếu đứng của \(j\) xuống đáy.

Ta có \( j_{1}\) là trung điểm của \( ab_{1}\), \( o_{1}j_{1}\) = \(ij ).

Giả sử \( \widehat{b_{1}ba}\) = \(30^0\).

Vậy: \(ab_1 = bb_1.tan 30^0\) = \( \frac{\sqrt{3}}{3}h = r\).

Xét tam giác vuông \(o_1j_1a\) tại \(j_1\) ta có:

\( o_{1}j^{2}_{1}\) = \( o_{1}a^{2}\) – \( aj^{2}_{1 } =\) \( r^{2} – {\left( {{r \trên 2}} \right)^2}=\) \( \frac{3}{4 }r^{2}\).

Vậy khoảng cách giữa \(ab\) và \(o_1o_2\) là: \( \frac{\sqrt{3}}{2}r\)

giaibaitap.me