Luyện tập: Giải bài 35 36 37 38 39 trang 94 95 sgk Toán 7 tập 1

Bài tập §5. Tiên đề Euclid về đường thẳng song song, Chương 1 – Đường thẳng vuông góc. Đường thẳng song song, một trong 7 tập sách giáo khoa toán học. Nội dung Giải bài 35 36 37 38 39 trang 94 95 SGK Toán 7 Tập 1 bao gồm các bài tổng hợp về công thức, lý thuyết và cách giải bài tập trong phần Hình học trong SGK Toán 7 giúp học sinh học tốt môn Toán lớp 7.

Bạn Đang Xem: Luyện tập: Giải bài 35 36 37 38 39 trang 94 95 sgk Toán 7 tập 1

Lý thuyết

1. Tiên đề Euclide

Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

2. Tính chất của hai đường thẳng song song

Nếu một đường thẳng cắt hai đường thẳng song song:

A. Hai góc so le trong thì bằng nhau.

Các góc của hai đồng vị bằng nhau.

Hai góc trong cùng phía phụ nhau.

3. Ví dụ

Trước khi bước vào Giải bài 35 36 37 38 39 trang 94 95 SGK Toán 7 Tập 1, chúng ta cùng nghiên cứu các ví dụ điển hình sau:

Ví dụ 1:

Hai đường thẳng song song x’x và y’y cắt tiếp tuyến tại hai điểm a và b. Hãy để là \(\widehat {xab}.\)

A. Tia có cắt đường thẳng y’y không? Tại sao?

Đối với \(\widehat {xab} = {80^0}.\) tính \(\widehat {acb}.\)

Xem Thêm: Bài thơ Đoàn thuyền đánh cá In trong tập Trời mỗi ngày lại sáng (1958)

Giải pháp:

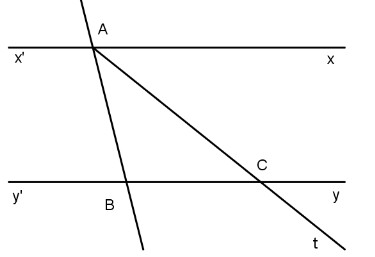
A. Giả sử chúng ta không cắt y’y

Suy ra ac//y’y. Theo tiên đề Euclid, ac trùng với x’x. Điều này là vô lý, vì vậy tia này phải cắt y’y tại c.

Ta có:

\(\widehat {xat} = \frac{1}{2}\widehat {xab} = \frac{1}{2}{.80^0} = {40^0} \) (at là tia phân giác của \(\widehat {xab}\)).

\(\widehat {xat} = \widehat {acb}\) (xen kẽ)

Vậy \(\widehat {acb} = {40^0}.\)

Ví dụ 2:

Cho hình bên, biết \(\widehat a = {50^0}\) và \(\widehat b = {140^0}\), ax // by’. Chứng minh rằng \(\widehat {aob} = {90^0}.\)

Xem Thêm: Bài thơ Đoàn thuyền đánh cá In trong tập Trời mỗi ngày lại sáng (1958)

Giải pháp:

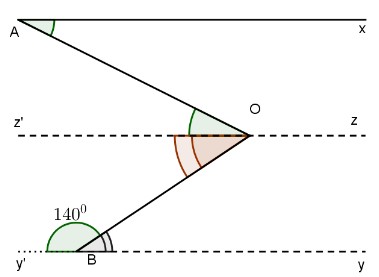
Qua đường oz // trục, ta có: \(\widehat {aoz} = \widehat {xao} = 50{}^0\) (góc so le)

Một lần nữa: \(\widehat {oby} = {150^0}\) \( \rightarrow \widehat {oby} = {180^0} – {140^0} = { 40 ^0}\) \(oz//ax \rightarrow oz//by\)

Xem Thêm: File excel mẫu theo dõi và quản lý hợp đồng bằng excel & hướng dẫn chi tiết

\( \rightarrow \widehat {boz’} = \widehat {oby} = {40^0}\) (góc so le)

Như vậy: \(\widehat {aoz} = \widehat {z’ob} = {50^0} + {40^0} = {90^0}\) hoặc \( widehat {aob} = {90^0}.\)

Ví dụ 3:

Đối với hình bên, biết ax // by. Chứng minh rằng \(\widehat a + \widehat b + \widehat c = {360^0}.\)

Xem Thêm: Bài thơ Đoàn thuyền đánh cá In trong tập Trời mỗi ngày lại sáng (1958)

Giải pháp:

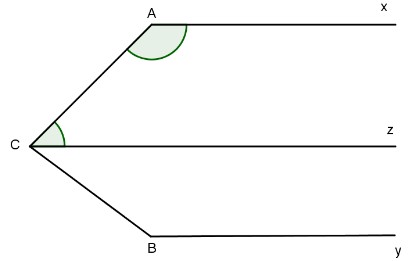
Qua dòng c cz // ta có cái rìu:

\(\widehat a + \widehat {acz} = {180^0}\) (góc kề bù)

Xem Thêm : Sài Gòn tôi yêu – tác giả, nội dung, bố cục, tóm tắt, dàn ý – Haylamdo

Một lần nữa: \(cz//ax \rightarrow cz//by \rightarrow \widehat b + \widehat {zcb} = {180^0}\) (góc bù bên trong)

\( \rightarrow \widehat a + \widehat b + \widehat {acz} + \widehat {zcb} = {360^0}\,\,\,\, hoặc \,\,\,\,\,\widehat a + \widehat b + \widehat c = {360^0}.\)

Ví dụ 4:

Đối với các góc quay được đo bằng \({30^0}\). Một điểm trên con bò. Bằng cách dựng tia a’y // oy và hợp với góc quay.

A. mát lạnh’.

Gọi ot và at’ lần lượt là tia phân giác của góc quay và góc mài. Chứng minh ot // tại’.

Xem Thêm: Bài thơ Đoàn thuyền đánh cá In trong tập Trời mỗi ngày lại sáng (1958)

Giải pháp:

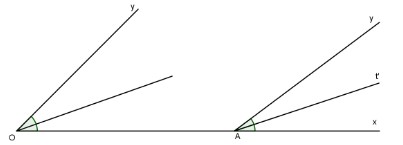
A. Làm đi’// oy

\( \rightarrow \widehat {xay’} = \widehat {rotation} = {30^0}\) (góc đẳng hướng)

Một lần nữa: \(\widehat {oay’} = \widehat {xay’} = {180^0}\) (góc kề)

\( \rightarrow \widehat {oay’} = {180^0} – \widehat {xay’} = {180^0} – {30^0} = {150^0}\ )

Làm \(\widehat {rotation} = \widehat {mill’}\) (đã chứng minh ở trên)

\( \rightarrow \frac{{\widehat {spin}}}{2} + \frac{{\widehat {xay}}}{2}\,\,or ,\,\widehat {{o_1}} = \widehat {{o_2}} \rightarrow \,ot\,//\,at’\) (góc đồng vị).

Ví dụ 5:

Gọi \(rotation = {120^0}\) và \(ot\) là tia phân giác của góc. Lấy điểm a trên tia oy và vẽ đường thẳng qua a tại ‘// ot.

A. Tính góc yat’

Dựng đường thẳng ax’ song song với ox. So sánh hai góc t’ax’ và tox.

Xem Thêm: Bài thơ Đoàn thuyền đánh cá In trong tập Trời mỗi ngày lại sáng (1958)

Giải pháp:

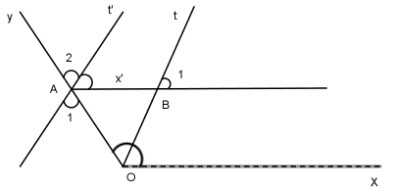
A. Thực hiện \(ot//\,at’ \rightarrow \widehat {{o_1}} = \widehat {{a_1}}\) (góc so le) trong đó \(\widehat {{ a_1 } } = \widehat {{a_2}}\) (nghịch đảo) nên \(\widehat {{a_2}} = \widehat {{o_1}}\)

Hoặc \(\widehat {yat’} = \widehat {yot} = {60^0}\) (vì ot là đường phân giác \(\widehat {rotation} = {120^0 )}\)).

Bởi vì \(\widehat {yat’} = \widehat {yot}\)(isotope)\( \rightarrow at’\,\, //ot.\)

ax’ cắt ot tại \(b \rightarrow \widehat {t’ax’} = \widehat {{b_1}}\) (đồng vị làm tại ‘// ot).

Mặt khác \(\widehat {tox} = \widehat {{b_1}}\) (đồng vị của ax’ //ox)

Suy ra \(\widehat {t’ac} = tox.\)

Dưới đây là hướng dẫn giải bài 35, 36, 37, 38, 39 trang 94, 95 SGK Toán 7 Tập 1. Các em hãy đọc kỹ bài 1 trước khi giải nhé!

Bài tập

giaibaisgk.com giới thiệu đến các bạn lời giải bài tập phần Hình học 7 đầy đủ với lời giải chi tiết trang 35 36 37 38 39 trang 94 95 SGK Toán Tập 1 Bài 5. Chương 1 Tiên đề Euclid về Đường thẳng Song song – Đường thẳng Vuông góc. Các đường thẳng song song để bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:

1. Giải bài 35 trang 94 SGK Toán 7 tập 1

Tam giác $abc$. Vẽ một đường thẳng $a$ qua đỉnh $a$ song song với $bc$ và một đường thẳng $b$ song song với $ac$ qua đỉnh $b$. Tôi có thể hỏi có bao nhiêu dòng $a$ và bao nhiêu dòng $b$ có thể được vẽ, và tại sao?

Giải pháp:

Theo tiên đề Euclid, qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Do đó:

– Qua đỉnh $a$, ta vẽ được một đường thẳng $a$ song song với $bc$.

– Qua đỉnh $b$ ta chỉ vẽ được đường thẳng $b$ song song với $ac$.

2. Giải bài 36 trang 94 SGK Toán 7 tập 1

Hình 23 cho thấy rằng $a // b$ và $c$ cắt $a$ tại $a$ và $b$ tại $b$. Điền vào chỗ trống (…) trong các câu sau:

a) $\widehat{a_1}$ = … (vì là một cặp góc so le trong)

Xem Thêm : Soạn bài Lục Vân Tiên cứu Kiều Nguyệt Nga siêu ngắn

b) $\widehat{a_2}$ = … (vì là một cặp góc đồng vị)

c) $\widehat{b_3}$ + $\widehat{a_4}$ = … (vì…)

d) $\widehat{b_4}$ = $\widehat{a_2}$ (vì…)

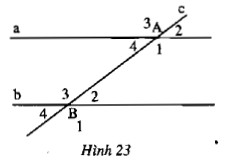
Giải pháp:

a) $\widehat{a_1}$ = $\widehat{b_3}$ (vì là một cặp góc so le trong)

b) $\widehat{a_2}$ = $\widehat{b_2}$ (vì là một cặp góc đồng vị)

c) $\widehat{b_3}$ + $\widehat{a_4}$ = $180^0$ (vì cả hai nằm trên cùng một mặt phẳng cạnh góc trong)

d) $\widehat{b_4}$ = $\widehat{a_2}$ (vì nó giống $\widehat{b_2}$ )

3. Giải bài 37 trang 95 SGK Toán 7 tập 1

Xem Thêm: TẢI 101+ hình ảnh cuộc sống bình yên đẹp giúp tâm thanh tịnh

Đối với Hình 24 $(a // b)$. Đặt tên cho cặp cạnh đều của hai tam giác $cab$ và $cde$.

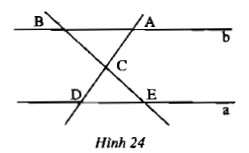
Giải pháp:

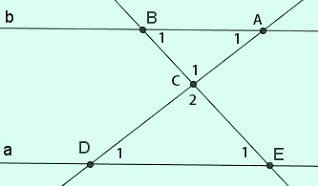
$\left.\begin{matrix} a // b\\ \widehat{b_1}\, và\, \widehat{e_1} so\,le\,in \end{matrix}\right\}$ ⇒ $\widehat{b_1}$ = $\widehat{e_1}$ ta có:

$\left.\begin{matrix} a // b\\ \widehat{a_1}\, và\, \widehat{d_1} so\,le\,in \end{matrix}\right\}$ ⇒ $\widehat{a_1}$ = $\widehat{d_1}$

$\widehat{c_1}$ = $\widehat{c_2}$ (hai góc đối đỉnh)

4. Giải bài 38 trang 95 SGK Toán 7 tập 1

Điền vào chỗ trống (…) trong bảng dưới đây:

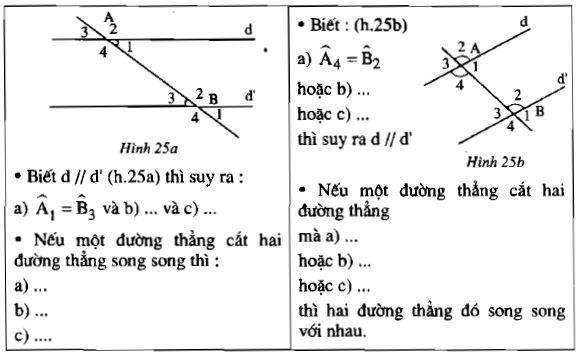
Giải pháp:

5. Giải bài 39 trang 95 SGK Toán 7 tập 1

Trắc nghiệm: Hình 26 cho thấy góc tù tại $d_1 // d_2$ và đỉnh $a$ bằng $150^0$

Tính góc nhọn tạo bởi $a$ và $d_2$.

Gợi ý: Tính góc nhọn $a$ theo độ.

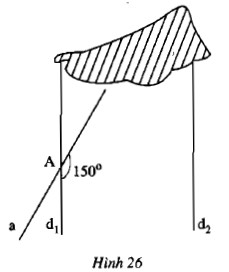
Giải pháp:

Ta có: \(\widehat {{a_1}}\) và \(\widehat {{a_2}}\) là hai góc kề bù nên:

\(\eqalign{ & \widehat {{a_1}} + \widehat {{a_2}} = {180^0} \cr & \rightarrow \widehat {{a_2} } = {180^0} – \widehat {{a_1}} = {180^0} – {150^0} = {30^0} \cr}\)

Vì d1 // d2 và \(\widehat {{a_2}}\) so le từ \(\widehat {{b_1}}\)

\( \rightarrow \widehat {{b_1}} = \widehat {{a_2}} = {30^0}\)

Vậy \(\widehat {{b_1}} = {30^0}\)

Trước:

• Giải bài 31 32 33 34 trang 94 SGK Toán 7 tập 1

Tiếp theo:

• Giải bài 40 41 Trang 97 SGK Toán 7 Tập 1

Xem thêm:

• Câu hỏi khác 7
• Học tốt vật lý lớp 7
• Học tốt môn sinh học lớp 7
• Học tốt ngữ văn lớp 7
• Điểm tốt môn lịch sử lớp 7
• Học tốt môn địa lý lớp 7
• Học tốt tiếng Anh lớp 7
• Học tốt môn tiếng Anh lớp 7 thí điểm
• Học tốt môn tin học lớp 7
• Học chăm chỉ gdcd lớp 7

Chúc các em thành công trong việc soạn sgk toán 7 có lời giải bài 35 36 37 38 39 trang 94 95 sgk toán 7 tập 1!

“Môn thể thao nào đã khó giabaisgk.com”