Bài tập §4. Tính chất ba đường trung tuyến của tam giác, Chương 3 – Mối quan hệ giữa các yếu tố trong tam giác – Đường trung tuyến của tam giác, SGK Toán 7 Tập II. Nội dung Giải bài 26 27 28 29 30 trang 67 SGK Toán 7 Tập 2 Tổng hợp các công thức, lý thuyết và phương pháp giải bài tập trong phần hình học trong SGK Toán giúp học sinh học tốt môn Toán 7.
Bạn Đang Xem: Luyện tập: Giải bài 26 27 28 29 30 trang 67 sgk Toán 7 tập 2
Lý thuyết
1. Trung tuyến của tam giác:
Đoạn thẳng m nằm giữa đỉnh a của tam giác abc và trung điểm m của cạnh bc gọi là trung tuyến.
Đường thẳng am còn gọi là đường trung tuyến của tam giác abc.
Mỗi tam giác đều có ba đường trung tuyến
2. Tính chất của 3 trung điểm của tam giác:
Lý thuyết:
Ba đường trung tuyến của một tam giác cùng đi qua một điểm.
Điểm cách mỗi đỉnh một khoảng bằng độ dài của đường trung tuyến \(\frac{2}{3}\) đi qua đỉnh đó.
Giao điểm của ba đường trung tuyến được gọi là trọng tâm của tam giác.
Dưới đây là lời giải các câu 26, 27, 28, 29, 30 trang 67 SGK Toán 2. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ và chi tiết các bài bài tập Hình học 7 Trang 26, 27, 28, 29, 30 và Trang 67 SGK Toán 2 Bài 4. Chương 3 là tính chất ba đường trung tuyến của tam giác – quan hệ giữa các yếu tố trong tam giác – hợp của tam giác để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 26 trang 67 SGK Toán 7 tập 2
Chứng minh định lý: Trong một tam giác cân, hai đường trung trực tương ứng với hai cạnh bằng nhau.
Giải pháp thay thế:
Δabc có trọng số a ab = ac.
Gọi m, n lần lượt là trung điểm của các cạnh ab, ac, suy ra:
an = bn = am = cm (=$\frac{1}{2}$ ab = $\frac{1}{2}$ ac)
Coi bam va can co:
Góc bình thường
ab = ac
Tôi là một
⇒ Δbam = Δcan (c.g.c) ⇒ bm = cn (dpcm)
2. Giải bài 27 tr.67 SGK Toán 7 2
Chứng minh điều ngược lại của định lý trên: Một tam giác cân nếu hai đường trung tuyến của nó bằng nhau.
Giải pháp thay thế:
Viết Δabc. m và n lần lượt là trung điểm của ac và ab và g là trọng tâm của tam giác.
Theo chủ đề: cn=bm.
Xem Thêm: Vì sao Trung cấp nghề Nha Trang và THPT Đại Việt bị cưỡng chế, giải thể?
Vì g là trọng tâm của tam giác abc nên: cg = $\frac{2}{3}$ cn; bg = $\frac{2}{3}$ bm.
Suy ra: cg = bg.
Ta có: ng = cn – cg = bm – bg = gm.
Xét tam giác bgn và cgm:
cg = bg (cmt)
$\widehat{g_1}=\widehat{g_2}$ (đối diện)
ng = gm (cmt)
$\rightarrow \delta bgn = \delta cgm (c-g-c)$
$\mũi tên phải bn = cm$
Xem Thêm : Ảnh buồn – Tổng hợp 100 hình ảnh buồn, cô đơn cực đẹp
với m, n là trung điểm của ab và ac nên ab = ac.
Vậy tam giác abc cân tại a
3. Giải bài 28 trang 67 SGK Toán 7 2
Cho tam giác cân có đường trung bình di tại d.
a) Chứng minh rằng dei = dfi.
b) Góc die và dif là gì?
c) Cho de = df = 13cm, ef = 10cm, tính độ dài trung tuyến di.
Giải pháp thay thế:
a) Think dei và dfi có:
de = df(Δdef cân bằng)
di là cạnh chung.
ie = if (di là trung vị)
⇒ Δdei = Δdfi (c.c.c)
b) Vì ∆dei = ∆dfi ⇒ \(\widehat{die} =\widehat{dif}\)
\(\widehat{die} +\widehat{dif}=180^0\) (liền kề)
Phải là \(\widehat{die} =\widehat{dif}= 90^0\)
c) i là trung điểm của ef nên ie = if = 5cm.
Δdie vuông tại i $de^2 = di^2 + ei^2$ (định lý pitago)
Xem Thêm: 110 trò chơi sinh hoạt vòng tròn
⇒ $di^2 = 13^2 – 5^2 = 144$
⇒ $di = 12.$
4. Giải bài 29 trang 67 sgk toán 7 tập 2
Gọi g là trọng tâm tam giác đều abc. Chứng minh: ga = gb = gc
Hướng dẫn: Áp dụng định lý bài tập 26.
Giải pháp thay thế:
Cho m, n, e là giao điểm của ag, bg, cg và bc, ca, ab.
Vì g là trọng tâm của abc
ga = \(\frac{2}{3}\)am; gb = \(\frac{2}{3}\)bn; gc = \(\frac{ 2}{3}\)ce (1)
Vì Δabc đều nên 3 trung tuyến ứng với 3 cạnh bc, ca, ab đều bằng nhau
⇒ am = bn = ce (2)
Từ (1), (2) ga = gb = gc
5. Giải bài 30 trang 67 sgk toán 7 tập 2
Gọi g là trọng tâm của tam giác abc. Lấy điểm g’ trên tia ag sao cho g là trung điểm của ag’.
a) So sánh các cạnh của tam giác bgg’ với đường trung tuyến của tam giác abc.
b) So sánh đường trung tuyến của tam giác bgg’ với các cạnh của tam giác abc.
Giải pháp thay thế:
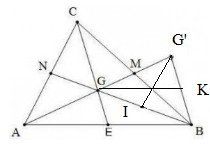
a)So sánh cạnh của bgg’ với trung vị của abc
bg cắt ac tại n
Xem Thêm : Truyện Chó sói và cừu non – bài học khi đối mặt với kẻ xấu
cg cắt ab tại e
g là trọng tâm của abc
⇒ \(ga = {2 \ hơn 3}am\)
ga = gg’ (g là trung điểm của ag’)
⇒ \(gg’ = {2 \hơn 3}sáng\)
Vì g là trọng tâm của abc \(gb = {2 \trên 3}bn\)
Nếu không:
m là trung điểm\(\left. {\ma trận{{gm = {1 \over 2}ag\left({tt} \right)} \cr {ag = gg’ \left( {gt} \right)} \cr} } \right\} ⇒ gm = {1 \trên 2}gg’\)
Xem Thêm: Người lái đò sông Đà – Tác giả tác phẩm (mới 2022) | Ngữ văn lớp 12
Do đó gmc=Δg’mb vì \(\left\{ {\ma trận{{gm = mg’} \cr {mb = mc} \cr {\widehat {gmc } = widehat {g’mb}} \cr } } \Có.\)
⇒ \({\ma trận{{bg’ = cg} \cr {{\rm{ }}cg = {2 \trên 3}ce} \cr} }\) (g là trọng tâm của tam giác abc)
\(⇒ bg’ = {2 \trên 3}ce\)
Vậy mỗi cạnh của bgg’ bằng trung vị của \({2 \trên 3}\) Δabc
b) So sánh trung tuyến của Δbgg’ với cạnh Δabc.
Ta có: bm là trung tuyến ∆bgg’
với m là trung điểm của bc nên \(bm = {1 \trên 2}bc\)
Vì \({ig = {1 \trên 2}bg}\) (vì i là trung điểm của bg)
\({gn = {1 \over 2}bg}\) (g là chìa khóa)
⇒ ig = gn
Do đó ∆igg’ = ∆nga (c.g.c) ⇒ \(ig’ = an ⇒ ig’ = {{ac} \trên 2}\)
Gọi k là trung điểm bg gk là trung điểm ∆bgg’
Vì \({ge = {1 \over 2}gc}\) (g là trọng tâm của tam giác abc)
bg’ = gc (đã chứng minh ở trên)
\(⇒ ge = {1 \ trên 2}bg\)
với k là trung điểm bg’ ⇒ kg’ = eg
Vì gmc = g’mb (đã chứng minh ở trên)
⇒ \(\widehat {gcm} = \widehat {g’bm}\) (xen kẽ)
⇒ ce // bg’ ⇒ \(\widehat {age} = \widehat {ag’b}\) (đồng vị)
Vậy ∆tuổi = ∆gg’k (c.g.c) ⇒ ae = gk
Sau đó \(ae = {1 \ trên 2}ab \rightarrow gk = {1 \trên 2}ab\)
Vậy mỗi đường trung tuyến ∆bgg’ bằng một nửa cạnh abc của tam giác bình thường.
Trước:
- Giải bài 23 24 25 trang 66 67 SGK Toán 7 Tập 2
- Giải bài 31 32 trang 70 SGK Toán 7 tập 2
- Câu hỏi khác 7
- Học tốt vật lý lớp 7
- Học tốt môn sinh học lớp 7
- Học tốt ngữ văn lớp 7
- Điểm tốt môn lịch sử lớp 7
- Học tốt môn địa lý lớp 7
- Học tốt tiếng Anh lớp 7
- Học tốt môn tiếng Anh lớp 7 thí điểm
- Học tốt môn tin học lớp 7
- Học chăm chỉ gdcd lớp 7
Tiếp theo:
Xem thêm:
<3
“Bài tập nào khó, đã có giabaisgk.com”
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục
