Giải bài 1, 2, 3, 4 trang 113, 114 Sách giáo khoa Hình học 11

Bài tập 1 trang 113 SGK hình học

Bạn Đang Xem: Giải bài 1, 2, 3, 4 trang 113, 114 Sách giáo khoa Hình học 11

Phát biểu nào sau đây đúng với ba mặt phẳng \((\alpha)\), \((\beta )\), \((\gamma )\)?

a) Nếu \((\alpha)\bot\beta\) và \((\alpha) // (\gamma)\) thì \((\beta )\bot(\gamma)\);

b) Nếu \((\alpha)\bot\beta\) và \((\alpha) \bot (\gamma)\) thì \((\ beta)//(\gamma)\).

NGƯỜI CHIẾN THẮNG

a) Đúng.

b) là sai.

bài giảng 2 trang 113 SGK hình học

Hai mặt phẳng \((\alpha)\) và \((\beta)\) vuông góc với nhau. Gọi \(\delta\) hai điểm \(a\) và \(b\) tại giao tuyến của hai mặt phẳng này sao cho \(ab=8cm\). Gọi \(c\) là một điểm trên \((\alpha)\) và \(d\) là một điểm trên \((\beta)\) sao cho \ ( ac \) và \(bd\) vuông góc với giao điểm \(\delta\) và \(ac=6cm\), \(bd=24cm\) . Tính độ dài của đoạn \(cd\).

NGƯỜI CHIẾN THẮNG

Xem Thêm: Hình ảnh “Vầng trăng sáng dịu hiền” và “trời xanh” trong bài viếng lăng Bác gợi lên cho em những cảm xúc và suy nghĩ gì

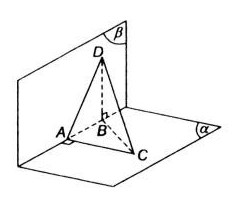
\(\ left.\matrix{ (\alpha) \bot (\beta) \hfill \cr ac \bot \delta \hfill \cr ac \tập hợp con (\alpha) \hfill \cr} \right\} \rightarrow ac \bot (\beta )\)

Vậy \(ac\bot ad\) hoặc tam giác \(acd\) nằm ở \(a\)

Áp dụng định lý Pitago cho tam giác\(acd\) ta được:

Xem Thêm : Hướng dẫn Giải bài 24 25 26 trang 63 64 sgk Toán 7 tập 1

$$d{c^2} = a{c^2} + a{d^2}(1)$$

Giả sử \(bd\) vuông góc với giao điểm nên \(bd\bot ab\) hoặc tam giác \(abd\) chính xác tại \(b\ ).

Áp dụng định lý Pitago cho tam giác \(abd\) ta được:

$$a{d^2} = a{b^2} + b{d^2}(2)$$

Suy ra từ (1) và (2): \(d{c^2} = a{c^2} + a{b^2} + b{d^2} = {6^2} + {8^2} + {24^2} = 676\)

\( \rightarrow dc = \sqrt {676} = 26cm\)

bài giảng 3 trang 113 SGK hình học

Cho tam giác \(abc\) trong mặt phẳng \((\alpha)\) tại \(b\). Đoạn thẳng \(ad\) vuông góc với \((\alpha)\) tại \(a\). Bằng chứng:

a) \(\widehat {abd}\) là góc giữa hai mặt phẳng \((abc)\) và \((dbc)\);

Xem Thêm: Yummy là gì

b) Mặt phẳng \((abd)\) vuông góc với mặt phẳng \((bcd)\);

c) \(hk//bc\) trong đó \(h\) và \(k\) là giao điểm của \(db\) và \(dc) ) mặt phẳng \((p)\) đi qua \(a\) và vuông góc với \(db\).

NGƯỜI CHIẾN THẮNG

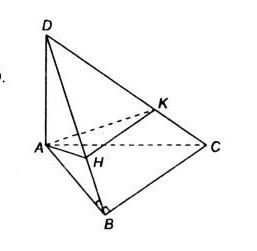
a) tam giác \(abc\) chính xác tại \(b\) nên \(ab\bot bc\) (1)

\(ad\) vuông góc với \((\alpha)\) nên \(ad\bot bc\) (2)

Từ (1) và (2) suy ra \(bc\bot (abd)\) suy ra \(bc\bot bd\)

Xem Thêm : 100 Hình xăm bít chân đẹp nhất 2022

\(\ left.\ma trận{ (abc) \cap (dbc) = bc \hfill \cr bd \bot bc \hfill \cr ab \bot bc \hfill \cr} \right\} \rightarrow \) Góc giữa hai mặt phẳng \((abc)\) và \((dbc)\) là góc \(\widehat {abd}\)

hai)

\(\ left.\ma trận{ bc \bot (abd) \hfill \cr bc \subset (bcd) \hfill \cr} \right\} \rightarrow (abd)\bot (bcd)\)

c)

Xem Thêm: SachHayOnline.com

Mặt phẳng \((p)\) đi qua \(a\) và vuông góc với \(db\) nên \(hk\bot bc\)

Trong \((bcd)\) có: \(hk\bot bc\) và \(bc\bot bd\) nên \(hk// bc\) )

Trang 4 114 Sách giáo khoa Hình học

Cho hai mặt phẳng \((\alpha)\), \((\beta)\) cắt nhau và điểm \(m\) không nằm trong \((\alpha ) ) thay vì trong \((\beta)\) . Chứng minh rằng qua điểm \(m\) tồn tại và duy nhất một mặt phẳng \((p)\) vuông góc với \((\alpha)\) và \((\beta ) \). Kết quả trên sẽ thay đổi như thế nào nếu \((\alpha)\) song song với \((\beta)\) ?

NGƯỜI CHIẾN THẮNG

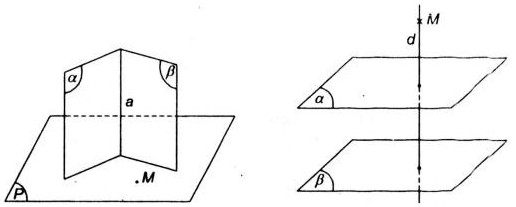
gọi \(a=(\alpha)\cap (\beta)\). Mặt phẳng \((p)\) đi qua \(m\) và vuông góc với \(a\).

Vì \(a\subset (\alpha)\) nên \((p)\bot (\alpha)\), \(a\subset (\beta) \) Vì vậy \((p)\bot(\beta)\)

Vậy qua \(m\) có một mặt phẳng \((p)\) vuông góc với \((\alpha)\) và \((\beta)\ ) .

Ngược lại: nếu bất kỳ \((p)\) nào đi qua \(m\) và vuông góc với \((\alpha)\) và \((\beta) ) Sau đó \((p)\bot a\). \((p)\) là duy nhất do tính duy nhất của mặt phẳng đi qua một điểm và vuông góc với đường thẳng đã cho.

Nếu \((\alpha)//(\beta)\) gọi \(d\) là một đường thẳng đi qua \(m\) và vuông góc với \(( \alpha )\) Sau đó, chúng tôi có \(d\bot (\beta)\). Vì vậy, mọi mặt phẳng chứa \(d\) đều vuông góc với \((\alpha)\) và \((\beta)\). Vậy khi \((\alpha)//(\beta)\) có vô số mặt phẳng \((p)\) đi qua \(m\) và vuông góc với (( alpha)\) và \((\beta)\).

giaibaitap.me