Hướng dẫn giải bài Ôn tập chương 2 – Hàm số bậc nhất, SGK Toán 9 Tập 1. Nội dung Giải bài 32 33 34 35 36 37 38 trang 61 62 SGK Toán 9 Tập 1 bao gồm tổng hợp các công thức, lý thuyết và phương pháp giải các bài tập đại số trong SGK Toán 9 giúp các em học tốt Toán lớp 9.
Bạn Đang Xem: Giải bài 32 33 34 35 36 37 38 trang 61 62 sgk Toán 9 tập 1
Tổng hợp kiến thức cần nhớ

Sau đây là Lời giải bài 32 33 34 35 36 37 38 trang 61 62 SGK toán 9 tập 1, các em đọc kĩ đề trước khi giải nhé!
Bài tập
giaibaisgk.com sẽ giới thiệu đến các bạn tài liệu Giải bài tập Đại số 9 đầy đủ và lời giải chi tiết hàm số bậc nhất chương 32 33 34 35 36 37 38 trang 61 62 SGK Toán 9 Tập 1 Ôn tập. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 32 trang 61 SGK Toán 9 Tập 1
a) Với giá trị nào của m thì hàm số bậc nhất $y = (m -1)x + 3$ đồng biến?
b) Với giá trị nào của k thì hàm nghịch biến của hàm số bậc nhất $y = (5 – k)x + 1$?
Giải pháp:
a) Hàm số $y = (m – 1)x + 3$ là hàm số bậc nhất của $x$ khi $m – 1 ≠ 0$ hoặc $m 1$, vì vậy Khi hệ số theo sau $x$ là dương, thì hàm này đồng biến.
Vậy $m – 1 > 0$ hoặc $m > 1$ thì hàm đồng biến.
b) Hàm $y = (5 – k)x + 1$ là hàm cấp một của $x$ khi $5 – k ≠ 0$ hoặc $k ≠ 5$, vì vậy Khi hệ số sau $x$ là âm, thì hàm nghịch biến.
Vậy $5 – k 5$ thì hàm số nghịch biến.
2. Giải bài 33 trang 61 sgk toán 9 tập 1
Với giá trị nào của m thì đồ thị hàm số $y = 2x + (3 + m)$ và $y = 3x + (5 – m)$ cắt nhau tại một điểm trên trục tung?
Giải pháp:
Các hàm \(y = 2x + (3 + m)\) và \(y = 3x + (5 – m)\) đều là hàm số bậc nhất của x, vì các hệ số của x không phải là 0.
Đồ thị của chúng là các đường thẳng cắt trục tung tại điểm b.
Như vậy, hai đường thẳng cắt nhau tại một điểm trên trục tung với điều kiện các góc của chúng bằng nhau: \(3 + m = 5 – m \rightarrow m = 1\).
Vậy khi $m = 1$ thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.
3. Giải bài 34 trang 61 SGK Toán 9 Tập 1
Tìm giá trị của a sao cho $y = (a – 1)x + 2 (a \neq 1)$ và $y = (3 – a)x + 1 (a \neq 3 ) $ là song song với nhau.
Giải pháp:
Hai dòng $y = (a – 1)x + 2$ và $y = (3 – a)x + 1$ bắt nguồn từ $b \neq b’$ khi $a = a’$ , cụ thể là:
$a – 1 = 3 – a 2a = 4 ⇔ a = 2$
Vậy khi $a = 2$, hai đường thẳng $y = (a – 1)x + 2$ và $y = (3 – a)x + 1$ song song.
4. Giải bài 35 trang 61 SGK Toán 9 Tập 1
Xác định $k$ và $m$ sao cho hai dòng sau trùng nhau:
$y = kx + (m – 2) (k \neq 0); y = (5 – k)x + (4 – m) (k \neq 5)$
Giải pháp:
Hai đường thẳng $y = kx + (m – 2)$ và $y = (5 – k)x + (4 – m)$ trùng nhau khi và chỉ khi:
$\begin{cases}k = 5 – k \\m – 2 = 4 – m\end{cases}$
⇔ $\begin{cases}k = \frac{5}{2} \\m = 3\end{cases}$
Xem Thêm: Tích phân là gì? Các công thức tính tích phân mà bạn nên biết
Vì vậy, khi $k = \frac{5}{2} $, $y = kx + (m – 2)$ và $y = (5 – k)x + (4 – m)$ Trùng đường thẳng $ m = 3$
5. Giải bài 36 trang 61 SGK Toán 9 Tập 1
Cho hai hàm bậc nhất $y = (k + 1)x + 3$ và $y = (3 – 2k)x + 1$
a) Giá trị của k là bao nhiêu thì đồ thị của hai hàm số là hai đường thẳng song song?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau?
c) Hai dòng trên có trùng nhau được không? Tại sao?
Giải pháp:
Hàm \(y = \left({k + 1} \right)x + 3\) có các hệ số \(a = k + 1,\,\,b = 3 )
Hàm \(y = \left({3 – 2k} \right)x + 1\) có các hệ số \(a’ = 3 – 2k,\,\, , b ‘ = 1\)
a) Khi đồ thị của hai hàm số là hai đường thẳng song song:
Xem Thêm : EYES CONTACT LÀ GÌ MÀ ĐA SỐ CHÚNG TA KHÔNG THỰC HIỆN ĐÚNG KHI GIAO TIẾP?
$\begin{cases} k + 1 \neq 0; 3 – 2k \neq 0 \\k + 1 = 3 – 2k\end{cases}$
$\begin{cases} k \neq -1; k \neq \frac{3}{2} \\k = \frac{2}{3}\end{ trường hợp}$
Vậy khi k = $\frac{2}{3}$, hai đường thẳng $y = (k + 1)x + 3$ và $y = (3 – 2k)x + 1$ song song với Mỗi dòng khác.
b) Đồ thị của hai hàm số là hai đường thẳng cắt nhau khi:
$\begin{cases} k \neq -1; k \neq \frac{3}{2} \\k \neq \frac{2}{3}\end {trường hợp}$
c) Ta có thể khẳng định ngay rằng các đường thẳng $y = (k + 1)x + 3$ và $y = (3 – 2k)x + 1$ không trùng nhau vì có $b \neq b’$
6. Giải bài 37 trang 61 SGK Toán 9 Tập 1
a) Vẽ hai hàm số sau trên cùng một mặt phẳng tọa độ:
$y = 0,5x + 2 (1); y = 5 – 2x (2)$
b) Gọi giao điểm của các đường thẳng $y = 0,5x + 2$ và $y = 5 – 2x$ lần lượt có trục hoành là a, b và gọi giao điểm của hai đường thẳng này là c . Tìm tọa độ của điểm $a,b,c$.
c) Tính độ dài đoạn thẳng $ab, ac$, $bc$ (đơn vị trên trục tọa độ là xăng-ti-mét) (làm tròn đến chữ số thập phân thứ hai)
d) Tính góc tạo bởi đường đẳng thức (1), (2) và trục ox (làm tròn đến phút)
Giải pháp:
a) Vẽ hai hàm:
Đồ thị của hàm số $y = 0,5x + 2$ là đường thẳng đi qua các điểm $(0; 2)$ và $(-4; 0)$
Đồ thị hàm số $y = 5 – 2x$ là đường thẳng đi qua các điểm $(0; 5)$ và $(2,5; 0)$

b) Điểm a là giao điểm của đường thẳng $y = 0,5x + 2$ với trục $ox$ nên $a(-4; 0)$
Điểm b là giao điểm của đường thẳng $y = 5 – 2x$ với trục $ox$ nên $b(2,5; 0)$
c là giao điểm của hai đường thẳng $y = 0,5x + 2$ và $y = 5 – 2x$ nên tọa độ của điểm $c$ là nghiệm của phương trình:
Xem Thêm: Tranh tô màu máy bay
$0,5x + 2 = 5 – 2x$
$ 2,5x = 3 ⇒ x = 1,2.$
Thay vì (1) hoặc (2), chúng ta nhận được $y = 2,6$
vậy tọa độ điểm $c(1,2; 2,6)$
c) Ta có $oa = 4; ob = 2,5$ nên $ab = 6,5$
Người đàn ông $ch \perp ab$. Ta có $oh = 1,2$ (đây là tọa độ của điểm c)
Suy ra $hb = ob – oh = 2,5 – 1,2 = 1,3$
$ha = ab – hb = 6,5 – 1,3 = 5,2$
Theo định lý Pitago ta có:
$ac^2$ = $ah^2$ + $hc^2$ = $(5,2)^2$ + $(2,6)^2$
$= 27,04 + 6,67 = 33,8$
Suy ra $ac = \sqrt{33,8} \xấp xỉ 5,81$
Tương tự ta có:
$bc^2$ = $bh^2$ + $hc^2$ = $(1,3)^2$ + $(2,6)^2$
$= 1,69 + 6,67 = 8,45$
Suy ra $bc = \sqrt{8,45} \xấp xỉ 2,91$
d) Gọi α và β lần lượt là các góc tạo bởi các đường thẳng (1), (2) và trục $ox$, ta có:
$tgα = \frac{ch}{ha} = \frac{2,6}{5,2} = 0,5$
$⇒ α \khoảng 26^033′$
Ta có:
$ tg\widehat{hbc} = \frac{ch}{hb} = \frac{2,6}{1,3} = 2 $
$⇒ \widehat{hbc} \khoảng 63^026′$
$β = 180^0 – 63^026′ = 116^034′$
7.Giải bài 38 trang 62 SGK Toán 9 Tập 1
a) Vẽ các hàm sau trên cùng một mặt phẳng tọa độ:
$y = 2x (1); y = 0,5x (2); y = -x + 6 (3)$
b) Gọi giao điểm của đường thẳng kẻ từ phương trình (3) và hai đường thẳng kẻ từ phương trình (1) và (2) lần lượt là a và b. Tìm tọa độ hai điểm a, b.
c) Tính các góc của tam giác $oab$.
Giải pháp:
Xem Thêm: Văn mẫu lớp 6: Kể lại truyện Thánh Gióng bằng lời văn của em 2 Dàn ý & 17 bài văn mẫu lớp 6
a) Các hàm vẽ:
Đồ thị hàm số $y = 2x$ qua các điểm $(1;2)$ và $(2;4)$
Đồ thị của hàm số $y = 0,5x$ qua các điểm $(2;1)$ và $(4;2)$
Đồ thị của hàm số $y = – x + 6$ qua các điểm $(0,6)$ và $(6;0)$
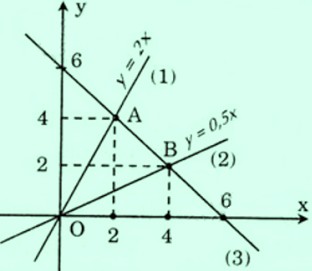
b)Ta có:
– Tọa độ của điểm a là nghiệm của phương trình:
$2x = -x + 6 ⇔ 3x = 6 ⇒ x = 2$
Thay $x = 2$ vào (1) ta được $y = 4$
Vậy tọa độ điểm $a(2; 4)$
– Tọa độ của điểm b là nghiệm của phương trình:
$0,5x = -x + 6 1,5x = 6 ⇒ x = 4$
Thay $x = 4$ vào (2) ta được $y = 2$
Vậy tọa độ điểm $b(4; 2)$
c)Ta có:
$oa^2$ = $2^2$ + $4^2 = 20 ⇒ oa = \sqrt{20}$
$ob^2$ = $4^2$ + $2^2 = 20 ob = \sqrt{20}$
Tam giác $aob$ có $oa = ob$ nên tam giác $aob$ cân tại $o$.
Ta có:
$tg\widehat{box}$ = $\frac{2}{4}$ = $\frac{1}{2}$
⇒ $\widehat{box} \khoảng 26^033′$
$tg\widehat{aox}$ = $\frac{4}{2} = 2$
⇒ $\widehat{aox} \khoảng 63^026′$
$\widehat{aob} = \widehat{aox} – \widehat{box} = 63^026′ – 26^033′ = 36^053′$
$\widehat{oab} = \widehat{oba} = 180^0 – 36^053′ = 71^033′$
Trước:
- Trả lời câu hỏi 1 2 Trang 59 60 SGK Toán 9 Tập 1
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học tốt tin học lớp 9
- Học tốt GDCD lớp 9
Xem thêm:
Chúc các bạn tham khảo và giải bài tập SGK Toán 9 bài 32 33 34 35 36 37 38 trang 61 62 SGK toán 9 tập 1 thành công!
“Môn thể thao nào đã khó giabaisgk.com”
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục