Hướng dẫn giải bài tập §3. Hàm Liên Tục, Chương 4. giới hạn, SGK Đại số và Giải tích 11. Nội dung Giải bài 1 2 3 4 5 6 trang 140 141 SGK Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, các phương pháp giải bài tập đại số SGK chứa số và phân tích giúp học sinh lớp 11 học tốt môn Toán môn Toán.
Bạn Đang Xem: Giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11
Lý thuyết
1. định nghĩa
Cho hàm số \(y = f(x)\) xác định trên khoảng k và \({x_0} \in k\)
Hàm số \(y = f(x)\) tại \({x_0} \leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f ( x ) = f({x_0})\)
Hàm số \(y = f(x)\) không liên tục tại \({x_0}\) Ta nói rằng hàm số không liên tục tại \({x_0}\)
Một hàm số \(y = f(x)\) liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số \(y = f(x)\) liên tục trên \(\left[{a;b} \right]\) nếu nó liên tục trên \(\ left ( {a ;b} \right)\) và
\(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a)\), \(\mathop {\ lim }\limits_{x \to {b^ – }} f(x) = f(b)\).
2. Một số định lý cơ bản
Quy tắc 1:
a) Hàm đa thức liên tục trên tập r.
b) Hàm số hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định.
Quy tắc 2:
Hàm số \(y = f(x),{\rm{ }}y = g(x)\) liên tục tại \({x_0}\). Khi đó tổng, hiệu và tích liên tục tại x0, và thương\(y = \frac{{f(x)}}{{g(x)}}\) liên tục nếu\(g( {x_0)} ) \ne 0\).
Định lý thứ ba
Cho hàm số f liên tục trên đoạn \(\left[{a;b} \right]\).
Nếu \(f(a) \ne f(b)\) và m nằm giữa \(f(a){\rm{ }},f(b)\) , thì ở đó có ít nhất một số \(c \in \left( {a;b} \right)\) sao cho \(f(c) = m{\rm{ }}\ )
Hậu quả:
Cho hàm số f liên tục trên đoạn \(\left[{a;b} \right]\).
Nếu \(f(a){\rm{ }}f(b) < 0\) thì tồn tại ít nhất một \(c \in \left( {a;b } \ phải)\) sao cho\(f(c) = 0\).
Lưu ý: Chúng ta có thể diễn đạt suy luận trên theo cách khác:
Cho hàm số f liên tục trên đoạn \(\left[{a;b} \right]\). Nếu \(f(a){\rm{ }}f(b) < 0\) thì phương trình \(f(x) = 0\) trong \(( a;b) ).
Dưới đây là câu hỏi và hướng dẫn trả lời luyện tập phần Hoạt động của học sinh trong SGK Đại số và Giải tích 11.
Câu hỏi
1. Trả lời câu 1 trang 135 SGK Đại số và Giải tích 11
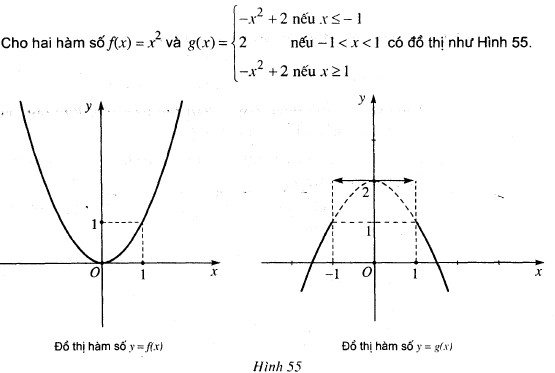
a) Tính giá trị của từng hàm số tại x = 1 rồi so sánh với giới hạn (nếu có) của hàm số đó tại x → 1;
b) Ghi chú thích đồ thị của mỗi hàm số tại điểm có tọa độ x = 1.
Trả lời:
a) Ta có: \(f(1) = {1^2} = 1 = \mathop {\lim }\limits_{x \to 1} f (x)\)
Xem Thêm: Lịch sử Trung Quốc : Phần 4 Nhà Hán
Vì \(x=1\) nên \(g(1) = -1^2+ 1 = -1 + 1 = 0\)
Một lần nữa: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim } limits_{x \to {1^ + }} \left( { – {x^2} + 2} \right) = 1\) và \(\mathop {\lim } giới hạn_{x \to {1^ – }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \left( 2 \right) = 2\) nên \(\mathop {\lim }\limits_{x \to {1^ – }} g\left( x \right) \ne mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)\) và không có giới hạn\(\mathop {\lim } giới hạn_{x \to 1} g\left( x \right)\)
b)Đồ thị của hàm số \(f(x)\) liên tục tại \(x = 1\)
Đồ thị hàm số \(g(x)\) ngắt tại \(x = 1\)
2. Trả lời 2 Trang 138 SGK Đại số và Giải tích 11
Trong biểu thức định nghĩa $h(x)$ đưa ra trong Ví dụ 2, số nào sẽ được thay thế bởi $5$ để thu được một hàm mới liên tục trên tập $r$ các số thực?
Trả lời:
Để hàm số liên tục trên \(\mathbb{r}\), nó phải nằm trong khoảng \(x = 1\) hoặc \(\mathop {\lim }\ giới hạn_{ x \to 1} h\left( x \right) = h\left( 1 \right)\) \( \leftrightarrow h\left( 1 \right) = 2 \ ).
Vậy ta cần thay số \(5\) bằng số \(2\) để hàm số liên tục trên \(\mathbb{r}\).
3. Trả lời bài 3 trang 138 SGK Đại số và Giải tích 11
Xem Thêm : Rét nàng Bân tháng 3 âm lịch và câu chuyện về Nàng Bân
Giả sử rằng hàm số $y = f(x)$ tiếp tục trên $[a; đoạn b]$ với các dấu ngược dấu của $f(a)$ và $f(b)$.
Điều gì sẽ xảy ra nếu đồ thị của hàm số cắt trục hoành tại một điểm trong khoảng $(a; b)$?
⦁ Bạn Hưng trả lời rằng: “Đồ thị của hàm số $y = f(x)$ phải cắt trục hoành $Ox$ tại một điểm duy nhất nằm trong khoảng $(a; b)$”. 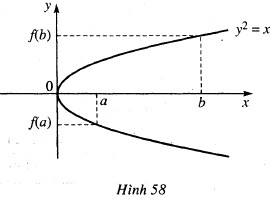
⦁ Bạn có thể xác nhận: “Đồ thị của hàm số $y = f(x)$ phải cắt trục hoành $ox$ ít nhất một chút gần với $(a; b)$”.
⦁ Các thành viên trong nhóm cho rằng: “Đồ thị của hàm số $y = f(x)$ có thể không cắt trục hoành trong khoảng $(a; b)$, chẳng hạn như parabol Hình (h.58) .
Câu trả lời nào của bạn đúng và tại sao?
Trả lời:
⦁ Bạn nói đúng, vì $f(a)$ và $f(b)$ trái dấu nên tồn tại ít nhất 1 giá trị của $x$ sao cho $f(x) = 0$, do đó đồ thị hàm số $ y = f(x)$ cắt trục hoành tại ít nhất 1 điểm.
⦁ Bạn đã nhầm, vì có thể có $2$ của $x$ sao cho $f(x) = 0$.
⦁ Parabola trong Hình 58 là đồ thị của hàm số y2 = x ⇒ đồ thị của hàm số $y = f(x$) sẽ nằm trên hoặc dưới nửa đường trục hoành.
Vậy thì $f(a)$ và $f(b)$ cùng dấu, mâu thuẫn với điều kiện $f(a)$ và $f(b)$ trái dấu. Ví dụ về thi đấu đồng đội
4. SGK Đại số và Giải tích Trang 139, câu 4, đáp án 11
Tìm hai số $a$ và $b$ thỏa mãn $1 <;a< b < 2$ sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng $(a; b)$.
Trả lời:
Ta có: \(f\left( x \right) = {x^3} + 2x – 5\).
Chọn \(a = \dfrac{5}{4},b = \dfrac{7}{4}\) để thỏa mãn \(1 < a < b < 2\ ).
Ta thấy: \(f\left( {\dfrac{5}{4}} \right) = – \dfrac{{35}}{{64}} 0\) nên \(f left ( {\dfrac{5}{4}} \right).f\left( {\dfrac{7}{4}} \right) < 0\).
Vì vậy, trong khoảng \(\left( {\dfrac{5}{4};\dfrac{7}{4}} \right)\) phương trình \(f\ left( x \right) = 0\) có ít nhất một nghiệm.
Dưới đây là hướng dẫn giải bài tập Đại số và Giải tích 11 SGK 1 2 3 4 5 6 trang 140 141. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn phương pháp Giải bài tập Đại số và Giải tích 11 đầy đủ và lời giải chi tiết Đại số và Giải tích 11 Bài 1 2 3 4 5 6 trang 140 141 SGK Bài 3. Hàm liên tục trong Chương 4 . chỉ để tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 1 trang 140 SGK Đại số và Giải tích 11
Xem Thêm: Top Những Câu Hỏi Và Câu Đố Về Ngày Trái Đất Hay Nhất
Dùng định nghĩa để xét tính liên tục của hàm số \(f(x) = x^3+ 2x – 1\) tại \(x_0= 3\).
Giải pháp thay thế:
Hàm số \(f(x) = x_3+ 2x – 1\) được xác định trên \(\mathbb r\) và \(x_0= 3 ∈ \mathbb r\).
\(\underset{x\rightarrow 3}{lim} f(x) =\) \(\underset{x\rightarrow 3}{lim}( x^3+ 2x – 1) = 3^3+ 2.3 – 1 = f(3)\) nên hàm số đã cho liên tục tại điểm \(x_0= 3\).
2. Giải bài 2 tr.141 SGK Đại số và Giải tích 11
a) Xét tính liên tục của hàm số \(y = g(x)\) tại \(x_0= 2\), biết
\(g(x) = \left\{\begin{matrix} \frac{x^{3}-8}{x- 2}; &x\neq 2 \ \ 5;& x=2 \end{matrix}\right.\).
b) Trong biểu thức phán đoán trên \(g(x)\) cần thay số \(5\) bằng một số bất kỳ để hàm số liên tục tại \(x_0= 2\ ).
Giải pháp thay thế:
a) Ta có \(\underset{x\rightarrow 2}{\lim} g(x) = \)\(\underset{x\ rightarrow 2}{lim}\) \(\frac{x^{3}-8}{x-2}\) = \(\underset{x\rightarrow 2}{lim}( x^2+2x + 4) = 2^2+2.2 +4 = 12\).
Vì \(\underset{x\rightarrow 2}{\lim} g(x) ≠ g(2)\) nên hàm \(y = g(x)\) là một đoạn trong \(x_0= 2\).
b) Để hàm số \(y = f(x)\) liên tục tại \(x_0= 2\) ta cần thay các số \( 5 \ ) nhân với số \(12\).
3. Giải bài 3 trang 141 SGK Đại số và Giải tích 11
Đối với hàm \(f(x) = \left\{\begin{matrix} 3x + 2; & x<-1\\ x^{2}-1 & x geq -1 \end{matrix}\right.\)
a) Vẽ đồ thị của hàm \(y = f(x)\). Từ đó nhận xét về tính liên tục của hàm số trên tập xác định của nó.
b) Hỗ trợ tuyên bố trên với bằng chứng.
Giải pháp thay thế:
a) Khi \(x<-1\) thì đồ thị hàm số là đường thẳng \(y=3x+2\), khi \( x \ ge – 1\) Đồ thị của hàm số là một parabola\(y=x^2-1\).
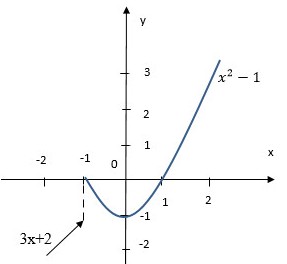
Xem Thêm : EXP là gì? Ý nghĩa EXP trong game và các lĩnh vực khác
Đồ thị hàm số \(y = f(x)\) là một đường không liền nét đứt tại \(x_0= -1\). Vậy hàm số đã cho liên tục trên các khoảng \((-∞; -1)\) và \((- 1; +∞)\).
b) Ta có:
Nếu \(x < -1\): \(f(x) = 3x + 2\) liên tục trên \((-∞; -1)\) (vì đây là hàm đa thức).
Nếu \(x>-1\): \(f(x) = x^2- 1\) liên tục trên \(((-1; +∞)\) (vì Đây là một hàm đa thức).
Trong \(x = -1\); ta có:
\(\underset{x\rightarrow -1^{-}}{lim} f(x) = \)\(\underset{x\rightarrow -1^{-}} {lim} (3x + 2) = 3(-1) +2 = -1\).
\(\underset{x\rightarrow -1^{+}}{lim} f(x) = \underset{x\rightarrow -1^{+}}{lim} (x^ 2- 1) = (-1)^2- 1 = 0\).
Bởi vì \(\underset{x\rightarrow -1^{-}}{lim} f(x) ≠ \underset{x\rightarrow -1^{+}}{lim} f( x)\) không được tồn tại \(\underset{x\rightarrow -1}{lim} f(x)\). Vì vậy, chức năng không liên tục tại \(x_0= -1\) .
4. Giải bài 4 trang 141 SGK Đại số và Giải tích 11
Đối với các hàm \(f(x) = \frac{x +1}{x^{2}+x-6}\) và \(g(x) = tanx + sin x ).
Xem Thêm: Bài 5: Ngày hội rừng xanh – Tiếng Việt lớp 3 tập 2 [ Kết Nối Tri Thức ]
Đối với mỗi hàm số, hãy xác định khoảng mà hàm số liên tục trên đó.
Giải pháp thay thế:
Hàm \(f(x) = \frac{x +1}{x^{2}+x-6}\) xác định nếu và chỉ khi \(x^2+ x – 6 ≠ 0 \leftrightarrow x ≠ -3\) và \(x ≠ 2\).
Hàm số \(f(x)\) liên tục trên các khoảng \((-∞; -3), (-3; 2)\) và \((2; +∞) )
Hàm \(g(x) = tanx + sinx\) xác định khi và chỉ khi \(tanx ≠ 0\leftrightarrow x ≠ \frac{\pi }{2} +kπ ) với \(k z\).
Hàm số \(g(x)\) liên tục trên khoảng\(( – \frac{\pi }{2}+kπ; \frac{\pi }{2} +kπ )\) và \(k ∈ \mathbb z\).
5. Giải bài 5 trang 141 SGK Đại số và Giải tích 11
Phát biểu sau đúng hay sai?
“Nếu hàm số \(y = f(x)\) liên tục tại \(x_0\) và hàm số \(y = g(x)\) không liên tục tại \ (x_0 \) Khi đó \(y = f(x) + g(x)\) là hàm số gián đoạn tại \(x_0\)”
Giải pháp thay thế:
Ý kiến đúng
Mặt khác, giả sử rằng \(y = f(x) + g(x)\) liên tục tại \(x_0\). Đặt \(h(x) = f(x) + g(x)\). Ta có \(g(x) = h(x) – f(x)\).
Vì \(y = h(x)\) và \(y = f(x)\) liên tục tại \(x_0\) nên sự khác biệt giữa chúng là hàm số \( y = g (x)\) phải liên tiếp tại \(x_0\). Điều này trái với giả định rằng \(y = g(x)\) không liên tục tại \(x_0\) .
6. Giải trang 141 Bài 6 SGK Đại số và Giải tích 11
Chứng minh đẳng thức:
a) \(2x^3- 6x + 1 = 0\) có ít nhất hai nghiệm;
b) \(cosx = x\) có nghiệm.
Giải pháp thay thế:
a) Hàm \(fx)=2x^3-6x + 1 = 0\) là một hàm đa thức và phải nằm trong \(\mathbb r\ ) .
Ta có: \(f(0).f(1) = 1.(-3) < 0\) nên nghiệm của phương trình nằm trong \((0; 1)\ ).
\(f(-2).f(0)=-5<0\) Vậy phương trình nằm trong khoảng \((-2; 0)\).
Vậy phương trình \(f(x) = 0\) có ít nhất hai nghiệm.
b) Hàm \(g(x) = cosx – x\) được xác định trên \(\mathbb r\) nên được xác định trên \(\ mathbb r Liên tục trên \).
Ngược lại, ta có \(g(0).g(\frac{\pi }{2}) = 1. (-\frac{\pi }{2}) < 0 \ ) nên phương trình đã cho có nghiệm trong khoảng \((0; \frac{\pi }{2})\).
Trước:
- Giải bài 1 2 3 4 5 6 7 Trang 132 133 SGK Đại số và Giải tích 11
- Ôn tập Chương iv: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 trang 141 142 143 144 SGK Đại số và Giải tích 11
- Câu hỏi khác 11
- Học tốt Vật lý lớp 11
- Học tốt môn sinh học lớp 11
- Học tốt ngữ văn lớp 11
- Điểm tốt môn lịch sử lớp 11
- Địa lý lớp 11
- Học tốt tiếng Anh lớp 11
- Học tốt môn Tiếng Anh lớp 11 thí điểm
- Học tốt môn Tin học lớp 11
- Học chăm chỉ môn gdcd lớp 11
Tiếp theo:
Xem thêm:
Chúc các em thành công trong quá trình tham khảo và Giải bài tập SGK toán 11 với Lời giải bài 1 2 3 4 5 6 trang 140 141 SGK Đại số và Giải tích 11!
“Môn thể thao nào đã khó giabaisgk.com”
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục




