Với tài liệu tóm tắt bài 4 Lý thuyết Toán lớp 10: Hệ bất phương trình bậc nhất hai ẩn sách được biên soạn chi tiết, liên kết chặt chẽ các kiến thức và bài tập tự luyện được chọn lọc giúp các em nắm vững các kiến thức quan trọng, ôn luyện học toán lớp 10.
Bạn Đang Xem: Lý thuyết Hệ bất phương trình bậc nhất hai ẩn (Kết nối tri thức 2022
Lý thuyết Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Một. Lý thuyết về bất phương trình bậc nhất hai ẩn số
1. Hệ bất phương trình bậc nhất hai ẩn số
– hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
– Cặp số x0;y0 là nghiệm của hai bất phương trình bậc nhất chưa biết của một hệ thì x0;y0 cũng là nghiệm của mọi bất phương trình trong hệ.
Ví dụ:
x+2y9 là hệ hai bất phương trình chưa biết gồm hai bất phương trình x+2y9.
x2+y2<5x−y>4 không phải là hệ bất phương trình bậc nhất một ẩn vì x2+y2<5 là bất phương trình bậc hai một ẩn.
– Cho hệ bất phương trình hai ẩn x+y>9x−y<9.
cặp (x; y) = (10; 2) là nghiệm 9 của bất phương trình x + y > và là nghiệm 9 của bất phương trình x – y <; nên cặp (x; y) = (10; 2) là các Giải pháp trên cho các hệ thống bất phương trình.
2. Biểu diễn lãnh thổ nghiệm của bất phương trình bậc nhất hai ẩn số trên mặt phẳng tọa độ
– Trong mặt phẳng tọa độ, tọa độ là tập điểm của nghiệm của hệ bất phương trình bậc nhất hai ẩn số, hai ẩn số là miền nghiệm của hệ bất phương trình.
-Miền nghiệm của hệ là giao của các miền nghiệm của bất phương trình trong hệ.
– Cách xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn số:
+ Trên cùng một mặt phẳng tọa độ, lần lượt xác định các miền nghiệm của hai bất phương trình bậc nhất một ẩn của hệ, gạch bỏ các miền còn lại.
+Miền không giao nhau là miền nghiệm của hệ bất phương trình đã cho.
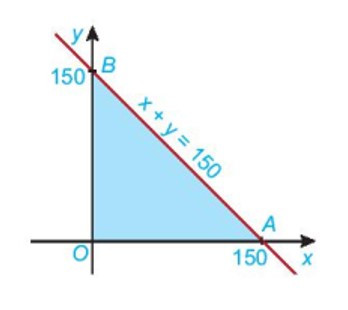
Ví dụ: Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn số: x≥0y≥0x+y≤150:
Bước đầu tiên: Xác định miền nghiệm d1 của bất phương trình x≥0 và gạch bỏ miền nghiệm còn lại.
– Đường thẳng x = 0 là trục oy.
– Miền nghiệm d1 của bất phương trình x≥0 là nửa mặt phẳng của cạnh oy nằm bên phải trục oy.
Bước 2: Tương tự, miền nghiệm d2 của bất phương trình y≥0 là cạnh bò của nửa mặt phẳng phía trên trục bò.
Bước thứ ba: nghiệm miền d3 của bất phương trình x + y 150:
– Vẽ đường thẳng d: x + y = 150.
– Vì 0 + 0 ≤ 150 luôn đúng nên tọa độ của điểm o(0; 0) thỏa mãn bất đẳng thức x + y ≤ 150.
Do đó, miền nghiệm d3 của bất phương trình x+y≤150 là nửa mặt phẳng có cạnh d chứa gốc tọa độ o.
Từ đó ta có miền nghiệm màu xanh lam, là giao điểm của miền nghiệm của các bất phương trình trong hệ.
3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn số
Lưu ý: Chứng minh tổng quát về giá trị lớn nhất (hoặc giá trị nhỏ nhất) của biểu thức fx;y=ax+by, trong đó x;y là tọa độ a1a2…an của điểm nằm trong miền đa giác, cụ thể là Một điểm bên trong hoặc trên một cạnh của đa giác, cho đến một trong các đỉnh của nó.
Ví dụ: Cho hệ bất phương trình bậc nhất hai ẩn số: x≥0y≥0x+y≤1002x+y≤120 và fx;y=3,5x+2y. Tìm giá trị lớn nhất của fx;y.
Hướng dẫn giải quyết:
Bước đầu tiên: Xác định miền nghiệm của hệ bất phương trình trên.
– Xác định miền nghiệm d1 của bất phương trình x 0.
– Đường thẳng x = 0 là trục oy.
– Miền nghiệm d1 của bất phương trình x≥0 là nửa mặt phẳng của cạnh oy nằm bên phải trục oy.
– Tương tự, miền nghiệm d2 của bất phương trình y ≥ 0 là nửa mặt phẳng của cạnh ox nằm phía trên trục ox.
– Miền nghiệm d3 của bất phương trình x + y 100:
Xem Thêm: Học bổng Vinuni – những điều cần biết
+ Vẽ đường thẳng d1: x + y = 100.
+ Vì 0 + 0 ≤ 100 luôn đúng nên tọa độ điểm o(0; 0) thỏa mãn bất đẳng thức x + y ≤ 100.
Như vậy, miền nghiệm d3 của bất phương trình x + y ≤ 100 chính là nửa mặt phẳng chứa cạnh d1 của gốc tọa độ o.
– Miền xác định là nghiệm d4 của bất phương trình 2x + y 120:
+ Vẽ đường thẳng d2: 2x + y = 120.
+ Vì 2. 0 + 0 ≤ 120 luôn đúng nên tọa độ điểm o(0; 0) thỏa mãn bất phương trình 2x + y ≤ 120.
Như vậy, miền d4 của bất phương trình 2x + y ≤ 120 là nửa mặt phẳng chứa cạnh d2 của gốc tọa độ o.
Từ đó ta có miền nghiệm màu xanh lam, là giao điểm của miền nghiệm của các bất phương trình trong hệ.
Miền gốc là tứ giác oabc với o(0,0), a(0;100), b(20;80), và c(60;0).
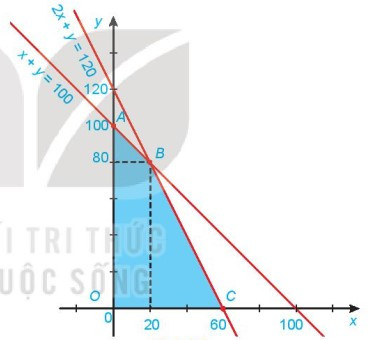
Bước thứ hai: tính giá trị của biểu thức f tại các đỉnh của tứ giác
f(o) = 0; f(a) = 200; f(b) = 230; f(c) = 210.
Xem Thêm : Soạn bài Khi con tu hú (Tố Hữu) | Ngắn nhất Soạn văn 8
Bước 3: So sánh các giá trị thu được ở Bước 2, ta được giá trị lớn nhất của fx;y là 230.
b. Bài tập tự rèn luyện
b1. Thực hành sáng tác
Bài 1 Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn số?
a) x0 b)x20 c) 2x+y>0 d) x−y1010
Hướng dẫn giải quyết
– Hệ bất phương trình x0 là hệ bất phương trình bậc nhất hai ẩn, vì tồn tại 2 bất phương trình x 0 đều là hệ bất phương trình bậc nhất hai ẩn.
– Hệ bất phương trình x20 không phải là hệ bất phương trình bậc nhất hai ẩn, vì tồn tại bất phương trình x2 <;0 không phải là bất phương trình bậc nhất hai ẩn.
– 2x+y>0 không phải là hệ bất phương trình bậc nhất hai ẩn, vì chỉ có một bất phương trình bậc nhất hai ẩn.
Hệ bất phương trình x−y1010 là hệ bất phương trình bậc nhất hai ẩn số, vì tồn tại 2 bất phương trình x − y 1010 đều là bất phương trình bậc nhất, và có hai ẩn số.
Vậy hệ x0 và x−y1010 là hệ bất phương trình bậc nhất hai ẩn.
bài 2.Cho hệ bất phương trình x≥0y≥0x+y≤1202x+y≤180
a) Tìm 2 nghiệm của hệ trên.
b) cho fx;y=2x+2y. Tìm giá trị lớn nhất của fx;y.
Hướng dẫn giải quyết
a) Chọn (x; y) = (1; 1).
Thay x = 1 và y = 1 vào bất đẳng thức x ≥ 0, ta được 1 ≥ 0, nghiệm nào đúng. Vậy cặp (1;1) là nghiệm của bất phương trình x≥0.
Thay x = 1 và y = 1 vào bất phương trình y ≥ 0 ta được 1 ≥ 0, vế nào đúng. Vậy cặp (1; 1) là nghiệm của bất phương trình y 0 .
Thay x = 1 và y = 1 vào bất đẳng thức x + y ≤ 120, ta được 1 + 1 ≤ 120, đúng. Vậy cặp (1; 1) là nghiệm của bất phương trình x + y 120 .
Thay x = 1 và y = 1 vào bất đẳng thức 2x + y ≤ 180, ta được 2. 1 + 1 ≤ 180 là đúng. Vậy cặp (1;1) là nghiệm của bất phương trình 2x + y 180 .
Vậy (x;y)=(1;1) là nghiệm của bất phương trình nhóm x≥0y≥0x+y≤1202x+y≤180.
Tương tự ta có thể chọn (x; y) = (2; 2) thỏa mãn mọi bất phương trình trong hệ đã cho. Vậy (2; 2) là nghiệm của bất phương trình nhóm x≥0y≥0x+y≤1202x+y≤180.
Vậy 2 nghiệm của hệ trên là (1; 1) và (2; 2).
hai)
– Xác định miền nghiệm d1 của bất phương trình x 0.
+ Đường thẳng x = 0 là trục tọa độ oy.
Xem Thêm: Hình ảnh “con tàu” trong Hai đứa trẻ của Thạch Lam | Văn mẫu 11
Miền d1 của bất phương trình + x≥0 là nửa mặt phẳng của cạnh oy nằm bên phải trục oy.
– Tương tự, miền nghiệm d2 của bất phương trình y ≥ 0 là nửa mặt phẳng của cạnh ox nằm phía trên trục ox.
– Miền nghiệm d3 của bất phương trình x + y 120:
+ Vẽ đường thẳng d1: x + y = 120.
+ Vì 0 + 0 ≤ 120 luôn đúng nên tọa độ điểm o(0; 0) thỏa mãn bất đẳng thức x + y ≤ 120.
Vậy miền nghiệm d3 của bất phương trình x + y ≤ 120 là nửa mặt phẳng chứa cạnh d1 của gốc tọa độ o.
– Miền xác định là nghiệm d4 của bất phương trình 2x + y 180:
+ Vẽ đường thẳng d2: 2x + y = 180.
+ Vì 2. 0 + 0 ≤ 180 luôn đúng nên tọa độ điểm o(0; 0) thỏa mãn bất phương trình 2x + y ≤ 180.
Vậy miền xác định của nghiệm d4 của bất phương trình 2x + y ≤ 180 là nửa mặt phẳng chứa cạnh d2 của gốc tọa độ o.
Từ đó ta được miền nghiệm vô hướng, là giao của các miền nghiệm của các bất phương trình trong hệ.
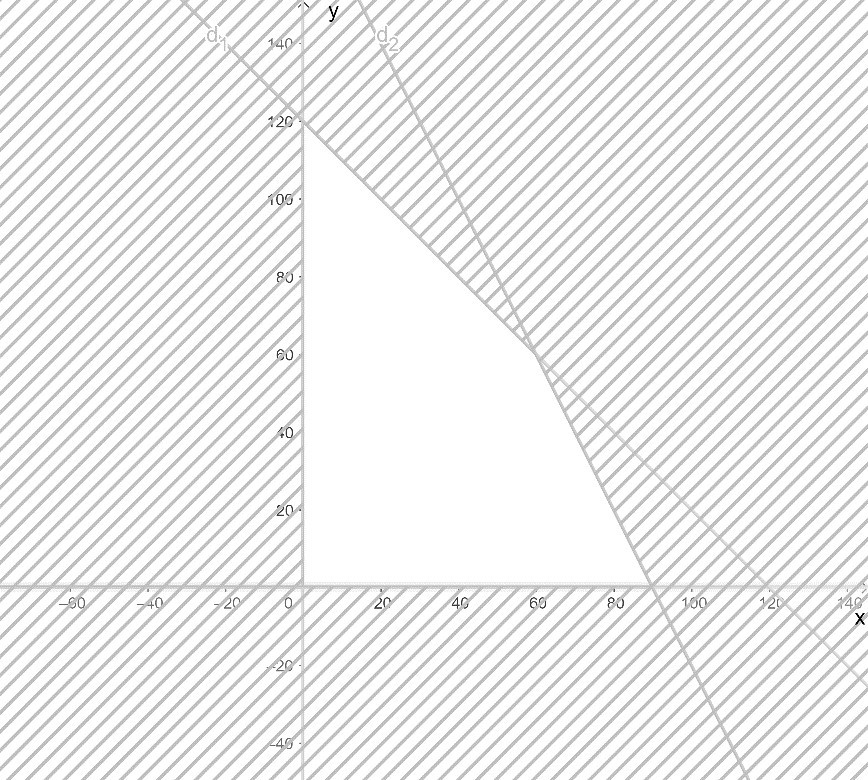
bài 3. Cho hệ bất phương trình x+2y−6. Đây có phải là hệ bất phương trình bậc nhất hai ẩn không? Hỏi x có thể nhận bao nhiêu giá trị nguyên khi y = 0?
Hướng dẫn giải quyết
x+2y−6 là hệ hai bất phương trình bậc nhất chưa biết, vì có 2 bất phương trình x + 2y <; – 6 là bất phương trình bậc nhất 2 ẩn .
Khi y = 0, hệ thức trở thành: x−6⇔−6<x<0
Vậy x có thể nhận các giá trị nguyên như: −5;−4;−3;−2;−1.
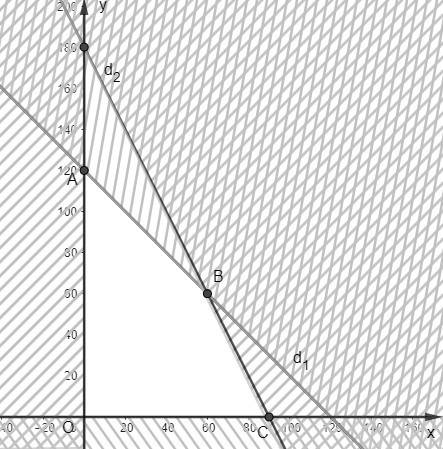
Tập nghiệm của hệ bất phương trình trên là tứ giác oabc, trong đó:
o(0;0), a(0;120), b(60;60), c(90,0).
Ta có: f(o) = 0; f(a) = 240; f(b) = 240; f(c) = 180.
Vì vậy, khi x;y=60;60 hoặc 0;120, giá trị lớn nhất của fx;y là 240.
b2. Câu hỏi trắc nghiệm
bài 4. Phát biểu sai được tìm thấy trong câu sau:
A. Hệ x+y≥−1y2−1≤0 không phải là hệ bất phương trình nhị phân bậc nhất;
Xem Thêm : Giải Sinh 9 Bài 1: Menđen và Di truyền học
Hệ x≥1+y5x+y<0 là hệ bất phương trình bậc nhất hai ẩn số;
Hệ x+1+y>0x2+y<0 là hệ bất phương trình bậc nhất hai ẩn số;
Hệ 12x+2y<7x+3y≤0 là hệ bất phương trình bậc nhất hai ẩn số;
Hướng dẫn giải quyết
Đáp án đúng là: c
+ Vì x+y≥−1y2−1≤0 chứa bất phương trình bậc hai y2 – 1 ≤ 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định rằng a là đúng.
+ Vì x≥1+y5x+y<0 chứa hai bất phương trình x ≥ 1 + y và 5x + y <; 0 đều là bất phương trình bậc nhất hai ẩn nên hệ này là hệ phương trình bậc nhất hai ẩn của bất bình đẳng.
Sau đó khẳng định rằng b là đúng.
+ Vì x+1+y>0x2+y<0 chứa bất phương trình bậc hai x2 + y <; 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.
Sau đó khẳng định c là sai.
+ Vì 12x+2y<7x+3y≤0 chứa hai bất phương trình 12x+y<7 và x + 3y≤0 đều là bất phương trình bậc nhất hai ẩn nên hệ này là hệ bất phương trình bậc hai ẩn .
Như vậy khẳng định d là đúng.
Vậy ta chọn đáp án c.
Câu 5. Hệ bất phương trình nào sau đây là nghiệm của cặp (0; -3)?
A. x−y≤1x+3y≤3x−4
2x−y>02x+y>1
−x−4y>−32x+y≤2
2x−y≤−35y≥−1
Hướng dẫn giải quyết
Đáp án đúng là:c
+ Ta có: 0 – (-3)= 3 > 1 và 0 + 3. (-3) < 3,0 – 4 (-9 < -4) là đúng.
Vậy (0; -3) không là nghiệm của bất phương trình x – y ≤ -1.
Vậy cặp (0; -3) không là nghiệm của bất phương trình x−y≤1x+3y≤3x−4.
+ Ta có: 2.0 – (-3) = 3 > 0 và 2.0 + (-3) = – 3 < 1.
Vậy (0; -3) không là nghiệm 1 của bất phương trình 2x + y >.
Cặp (0; -3) do đó không phải là nghiệm của bất phương trình 2x−y>02x+y>1.
+ Ta có: -0 – 4.(-3)= 12 > – 3 và 2.0 + (-3) = – 3 < 2.
Vậy (0; -3) là nghiệm của hai bất phương trình -x -4y >; -3 và 2x + y 2.
Vậy cặp (0; -3) là nghiệm của bất phương trình −x−4y>−32x+y≤2.
+ Ta có: 2.0 – (-3)= 3 > – 3 và 5. (-3) = -15 <- 1.
Vậy (0; -3) không là nghiệm của hai bất phương trình 2x – y ≤ -3 và 5y ≥ -1.
Vậy cặp (0; -3) không là nghiệm của bất phương trình 2x−y≤−35y≥−1.
Vậy cặp (0; -3) là nghiệm của bất phương trình −x−4y>−32x+y≤2.
Vậy ta chọn đáp án c.
Bài tập 6. Phần tô đậm (không có viền) trong hình dưới đây biểu thị tập nghiệm của hệ bất phương trình sau?
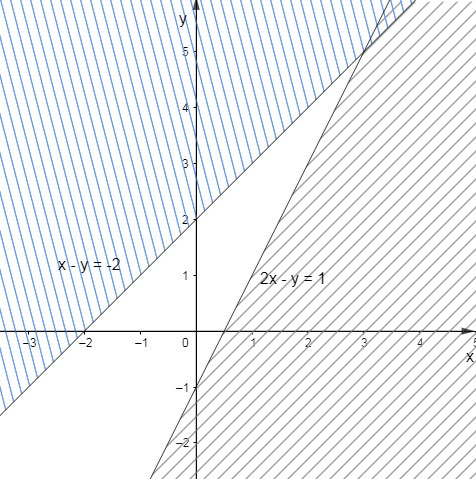
A. x−y≥−22x−y≥1
x−y>−22x−y<1
x−y1
x−y<−22x−y<1
Hướng dẫn giải quyết
Đáp án đúng là: b
Đường thẳng x – y = -2 chia mặt phẳng tọa độ làm đôi.
Xét điểm o(0; 0), ta có: 0 – 0 = 0 > -2 .
Mặt khác, điểm o thuộc miền nghiệm của bất phương trình cần tìm. Vậy ta có bất phương trình bậc nhất của hệ x – y >;-2.
Đường thẳng 2x – y = 1 chia nửa mặt phẳng tọa độ.
Xét điểm o(0; 0), ta có: 2.0 – 0 = 0 <; 1.
Mặt khác, điểm o thuộc miền nghiệm của bất phương trình cần tìm. Vậy ta có bất phương trình bậc 2 của hệ 2x – y <;1.
Suy ra rằng hệ thức bạn đang tìm là: x−y>−22x−y<1
Ta chọn đáp án b.
Nguồn: https://anhvufood.vn
Danh mục: Giáo Dục
- Sàn đấu ca từ: Thanh Duy hát sai hit của Sỹ Luân, Đào Bá Lộc bối rối sợ người yêu ghen vì được trai đẹp ôm
- Top 5 Loại Chăn lông cừu tốt nhất hiện nay 2022
- Công thức nấu lẩu cua đồng theo kiểu miền Bắc ngon bổ dưỡng
- So sánh hình ảnh đoàn quân trong Tây Tiến và Việt Bắc (5 Mẫu)
- Giấy can là gì? Lý giải nguyên nhân giấy can có tính trong
