Luyện tập: Giải bài 30 31 32 trang 116 sgk Toán 9 tập 1

Bài tập §6. Tính chất của hai tiếp tuyến cắt nhau, Chương 2 – Đường tròn, SGK Toán 9, tập 1, tr. Nội dung Giải bài 30 31 32 trang 116 SGK Toán 9 Tập 1 Các công thức, lý thuyết và phương pháp giải phần hình học trong SGK Toán 9 được tổng hợp toàn diện, giúp học sinh học tốt môn Toán lớp 9.

Bạn Đang Xem: Luyện tập: Giải bài 30 31 32 trang 116 sgk Toán 9 tập 1

Lý thuyết

1. Định lý hai tiếp tuyến cắt nhau

Định lý: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

Điểm cách đều cả hai điểm tiếp xúc.

Tia kẻ từ điểm này qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

Tia kẻ từ tâm qua điểm là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

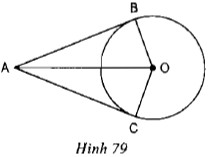
– Góc tạo bởi hai tiếp tuyến ab và ac là góc bac

– Góc tạo bởi hai bán kính đi qua tiếp điểm là góc

2. Đường tròn nội tiếp tam giác

Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, tam giác gọi là đường tròn ngoại tiếp.

Tâm đường tròn nội tiếp của một tam giác là giao điểm của các đường phân giác trong của tam giác đó.

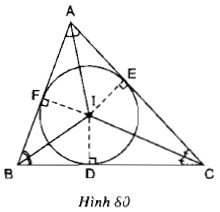
3. Đường tròn là tiếp tuyến của tam giác

Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với kéo dài hai cạnh còn lại gọi là đường tròn tiếp xúc với tam giác.

Tâm đường tròn ngoại tiếp góc a là giao điểm của hai đường phân giác khác góc b và góc c hoặc là giao điểm của tia phân giác của góc a và tia phân giác của góc b (hoặc c).

p>

Có một tam giác có 3 đường tròn tiếp xúc với tam giác.

Dưới đây là lời giải câu 30, 31, 32 trang 116 SGK Toán 1. Các em đọc kỹ câu hỏi trước khi giải nhé!

Bài tập

giaibaisgk.com giới thiệu đến các bạn lời giải phần bài tập Hình học 9 đầy đủ và lời giải chi tiết bài 30 31 32 trang 116 SGK Toán Tập 1 Bài 6. Chương Hai – Tính chất hai tiếp tuyến cắt nhau trong một đường tròn dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:

1. Giải bài 30 trang 116 SGK Toán 9 Tập 1

Xem Thêm: Bên bụi tre làng

Cho nửa đường tròn tâm o có đường kính ab (đường kính của đường tròn chia đường tròn thành hai nửa đường tròn). Gọi ax, by là tia vuông góc với ab (ax, by và nửa đường tròn cùng nằm trong nửa mặt phẳng có cạnh ab). Qua điểm m nằm trên nửa đường tròn (m khác a và b), kẻ tiếp tuyến của nửa đường tròn và cắt ax, by lần lượt tại c, d. Bằng chứng:

a) $\widehat{cod} = 90^0$

b) $cd = ac + bd$

c) Tích $ac.bd$ và điểm $m$ không đổi khi chuyển động trên nửa đường tròn.

Giải pháp:

Xem Thêm : Luyện từ và câu: Từ đồng âm trang 51 SGK Tiếng Việt 5 tập 1

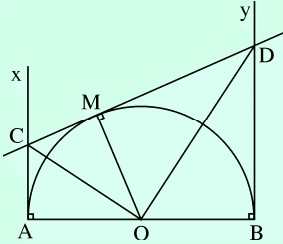
a) Ta có $oc$ là tia phân giác của góc $aom$ (vì $ab, ac$ là hai tiếp tuyến của đường tròn (o)$)

Tương tự, $od$ là tia phân giác của góc $bom$ (tính chất của hai tiếp tuyến cắt nhau)

góc $aom$ và góc $bom$ là hai góc bù nhau

Suy ra $oc \perp od$ hoặc $\widehat{cod} = 90^0$ (dpcm)

b)Ta có: $cd = cm + md$

$cm = ac, md = bd$ (tính chất của hai tiếp tuyến cắt nhau)

Vậy $cd = ac + bd (dpcm)$

c) Trong tam giác vuông $cod$ có:

$om \perp cd$ (thuộc tính tiếp tuyến)

$⇒ cm.md = om^2$ (tam giác vuông)

hoặc $ac.bd = r^2$

Xem Thêm: Tập làm văn lớp 4: Tả cây hoa mai (Dàn ý 26 mẫu) Bài văn tả hoa mai lớp 4

Trong đó $r$ là bán kính của hình tròn $(o)$ nên nó không thay đổi.

Vậy khi điểm m di chuyển trên nửa đường tròn thì $ac.bd$ sẽ không thay đổi. (dpcm)

2. Giải bài 31 trang 116 sgk toán 9 tập 1

Trong Hình 82, tam giác $abc$ ngoại tiếp đường tròn $(o)$.

a) Chứng minh: $2ad = ab + ac – bc$.

b) Tìm các quan hệ đồng dạng như ở a).

Giải pháp:

a) Theo tính chất hai tiếp tuyến cắt nhau, ta có:

$ad = af, bd = be, cf = ce.$

Do đó:

$ab + ac – bc = (ad + db) + (af + fc) – (be + ec)$

$= ad + db + ad + ce – bd – ec = 2ad$

Xem Thêm : Hướng dẫn Giải bài 10 11 trang 104 sgk Toán 9 tập 1

Vậy $2ad = ab + ac – bc (dpcm)$

b) Mối quan hệ tương tự như a) là:

$2be = ba + bc – ac$

$2cf = ca + cb – ab$

3. Giải bài 32 trang 116 SGK Toán 9 Tập 1

Tam giác đều $abc$ ngoại tiếp đường tròn bán kính $1cm$. Diện tích tam giác $abc$ bằng:

(a) 6 $cm^2$ ; (b) $\sqrt{3}$ $cm^2$ ; (c) $\frac{3\sqrt{3}}{4}$ $cm^2$; (d) 3$\sqrt{3}$ $cm^2$.

Xem Thêm: Phân tích người đàn bà hàng chài siêu hay (18 Mẫu)

Hãy chọn câu trả lời đúng.

Giải pháp:

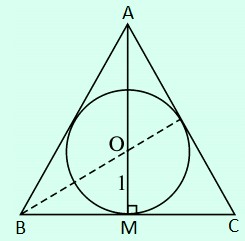
Gọi $o$ là tâm đường tròn nội tiếp tam giác $abc và m$ là tiếp tuyến ($m \in bc$)

Ta có $om = 1cm ⇒ am = 3cm$ (theo thuộc tính trung vị)

Ta có $\widehat{c} = 60^0$ (vì tam giác $abc$ là tam giác đều)

Áp dụng các tỉ số lượng giác vào tam giác vuông $amc$, ta có:

$tg \widehat{c} = \frac{am}{mc}$

$⇒ mc = \frac{am}{tg \widehat{c}} = \frac{3}{\sqrt{3}} = \frac{3\sqrt{3}} {3} = \sqrt{3}$

Vậy $mc = \sqrt{3} (cm)$

$⇒ bc = 2mc = 2\sqrt{3} (cm)$

$s_{\delta abc} = \frac{1}{2}bc.am = \frac{2\sqrt{3}.3}{2} = 3\sqrt{3} (cm^2)$.

Vậy câu trả lời d là đúng.

Trước:

• Giải bài 26 27 28 29 trang 115 116 SGK Toán 9 Tập 1

Tiếp theo:

• Giải bài 33 Trang 34 119 SGK Toán 9 Tập 1

Xem thêm:

• Câu hỏi khác 9
• Học tốt vật lý lớp 9
• Học tốt môn sinh học lớp 9
• Học tốt ngữ văn lớp 9
• Điểm tốt môn lịch sử lớp 9
• Học tốt môn địa lý lớp 9
• Học tốt tiếng Anh lớp 9
• Tiếng Anh lớp 9 thí điểm
• Học tốt tin học lớp 9
• Học tốt GDCD lớp 9

<3

“Môn thể thao nào đã khó giabaisgk.com”