Hình chóp đều tam giác, hình chóp đều tứ giác

Định nghĩa Kim tự tháp là gì? một kim tự tháp đa giác thường xuyên là gì? Các tính chất của kim tự tháp quy tắc là gì? Các dạng bài tập hình chóp đều? … Trong bài viết chi tiết dưới đây hãy cùng chúng tôi tìm hiểu ngay chủ đề và một số kiến ​​thức liên quan về kim tự tháp nhé!

Bạn Đang Xem: Hình chóp đều tam giác, hình chóp đều tứ giác

Hình chóp đều là gì? Hình chóp đa giác đều

Định nghĩa của một kim tự tháp tích cực là gì?

Hình chóp đều (hình chóp đa diện đều) là hình chóp có các mặt bên là tam giác cân và đáy là đa giác đều (tam giác đều, hình vuông,…)

Tính chất: Đáy cao của hình chóp đa giác đều là tâm đáy.

Vì vậy, để một hình chóp là một hình chóp thì phải thỏa mãn hai điều kiện sau:

• Đáy của hình chóp đó là một đa giác đều (tam giác đều, vuông,…)
• Đáy cao nhất của kim tự tháp là tâm của đáy

Một số thuật ngữ quan trọng có liên quan

• Tâm của tam giác đều là giao điểm của ba đường trung tuyến, đường cao, đường trực tâm và đường phân giác trong.
• Tâm hình vuông là giao điểm của hai đường chéo.
• Hình chóp tam giác đều là hình chóp đều có đáy là tam giác (có các cạnh bên là tam giác không đều).
• Hình chóp tứ giác đều là hình chóp có đáy là tứ giác đều (lúc này đáy là hình vuông và các cạnh bên là tam giác cân).

Công thức thể tích của hình chóp đều

Thể tích hình chóp đều: \(v = \frac{1}{3}.s.h\)

Trong đó: s là diện tích đáy, h là chiều cao

Thể tích của hình chóp cụt dương: \(v = \frac{1}{3}.h.(b + b’ + \sqrt{b.b’}) )

Ở đâu:

b và b’ lần lượt là diện tích của đáy lớn và đáy nhỏ của hình chóp cụt đều.

Xem Thêm: Đề cương ôn thi học kì 1 môn Ngữ văn lớp 9 năm 2021 – 2022 Ôn tập học kì 1 lớp 9 môn Ngữ văn

h là chiều cao (khoảng cách giữa hai đáy).

Diện tích hình chóp đều



• Ta có hình chóp có tổng s bằng tổng s xung quanh và s đáy.
• Đối với hình chóp, để tính diện tích xung quanh ta cần tính tổng các cạnh.
• Để tính diện tích xung quanh hình chóp cụt, chúng ta cần tính s trên một cạnh và nhân với số cạnh hoặc lấy s xung quanh hình chóp lớn trừ s xung quanh hình chóp nhỏ.

Lý thuyết kim tự tháp tam giác đều là gì?

Định nghĩa hình chóp tam giác đều?

Kim tự tháp tam giác đều là hình chóp có đáy là tam giác đều với ba cạnh (hoặc các cạnh) bằng nhau.

Xem Thêm : Mẫu Chữ Ký Tên Thành, Thạnh Đẹp ❤️️ Hợp Phong Thủy



Tính chất của hình chóp tam giác đều

• Đáy là tam giác đều
• Tất cả các bên đều bình đẳng
• Tất cả các cạnh là tam giác đều
• Chân cao trùng với tâm mặt đáy (tâm mặt đáy là tâm tam giác abc)
• Các cạnh và đáy tạo thành các góc bằng nhau
• Tất cả các cạnh và đáy tạo thành các góc bằng nhau.

***Lưu ý:

• Tâm của tam giác đều là giao điểm của ba đường trung tuyến là đường cao, đường trung tuyến và đường phân giác trong.
• Tâm hình vuông là giao điểm của hai đường chéo.

Thể tích tam giác đều

Phương pháp tính thể tích của khối nón tam giác đều sabc là \(v_{sabc} =\frac{1}{3}.s_{\delta abc}.so\)

Trong đó: \(s_{\delta abc}\) là diện tích đáy của tam giác đều abc.

Đối với đường cao kẻ từ s đến tâm o đáy abc cũng vậy.

Ví dụ 1: Cho hình chóp tam giác đều sabc có đáy a và cạnh 2a. Chứng minh rằng chân đường cao vẽ từ hình chóp s là tâm của tam giác đều abc. Tính thể tích của đỉnh sabc đều.

Xem Thêm: Cảm nhận của anh, chị về nhân vật Ngô Tử Văn trong Chuyện chức phán sự đền Tản Viên



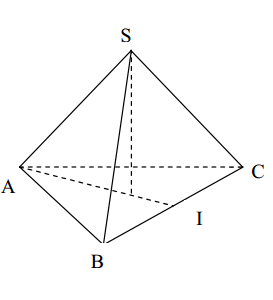
Giải pháp

Dựng \(nên \perp \delta abc\), ta có sa = sb = sc suy ra oa = ob = oc nên o là tâm tam giác đều abc. Ta có: \(ao=\frac{2}{3}ah=\frac{2}{3}\frac{a\sqrt{3}}{2}=\frac{a sqrt{3}}{3}\)

Tam giác đều abc Vậy tam giác vuông có: \(so^{2}=sa^{2}-oa^{2}=\frac{11a^{2}}{3}\ )

=> \(so=\frac{a\sqrt{11}}{\sqrt{3}}\) => \(v=\frac{1}{3}s_ {\delta abc}.so=\frac{a^{3}\sqrt{11}}{12}\)

Lý thuyết hình chóp tứ giác đều là gì?

Định nghĩa hình chóp tứ giác đều là gì?

Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và có chiều cao đi qua tâm (giao điểm của hai đường chéo của hình vuông) p>



Tính chất của hình chóp tứ giác đều

• Đáy là hình vuông.
• Tất cả các bên đều bình đẳng.
• Tất cả các cạnh là tam giác đều.
• Các đường gờ cao trùng với tâm của mặt đáy.
• Mọi góc tạo bởi cạnh và đáy đều bằng nhau.
• Tất cả các cạnh và đáy tạo thành các góc bằng nhau.

Thể tích của hình chóp tứ giác đều

Xem Thêm : Tiếng Việt lớp 5 tập 2 Tuần 28 trang 103 – Ôn tập giữa học kì 2 Tiết 7

Thể tích của hình chóp tứ giác đều sabcd là: \(v=\frac{1}{3}.s_{abcd}.so\) trong đó: \(s_{abcd}\) là diện tích hình vuông abcd

Tương tự với đường cao từ o đến tâm đáy abcd

Ví dụ 2: Cho tất cả các tứ diện hình chóp đều sabcd có cạnh dài bằng a. Chứng minh rằng sabcd là một đỉnh của tứ giác đều. Tính thể tích của khối nón sabcd.

Xem Thêm: Người mẹ vĩ đại của Chủ tịch Hồ Chí Minh



Giải pháp

Xây dựng \(so \perp (abcd)\)

Ta có sa = sb = sc = sd nên oa = ob = oc = od

=> abcd là hình thoi có đường tròn ngoại tiếp nên abcd là hình vuông. Ta có \(sa^{2}+sb^{2}=ab^{2}+bc^{2}=ac^{2}\) nên \(\delta asc\) là một vuông tại s

=> \(os=\frac{a\sqrt{2}}{2}\)

=>\(v=\frac{1}{3}.s_{abcd}.so=\frac{1}{3}.a^{2}.\frac{a sqrt{2}}{2}=\frac{a^{3}\sqrt{2}}{6}\)

Sự khác nhau giữa hình chóp tam giác đều và hình chóp tứ giác đều

• Hình chóp tam giác đều là hình chóp đều có đáy là tam giác (các cạnh bên là tam giác cân và tam giác không đều).
• Tứ giác đều theo định nghĩa là một hình chóp có đáy là tứ giác đều (bây giờ đáy là hình vuông và các cạnh là tam giác cân).

Nêu mối quan hệ giữa hình chóp tam giác đều và hình tứ diện đều?

• Hình chóp tam giác đều có tứ diện đều cạnh không bằng đáy, điều kiện thêm đối với các đỉnh của tam giác đều là cạnh bằng đáy là tứ diện đều.
• Tứ diện đều là một loại hình chóp tam giác đều đặc biệt (có thêm các cạnh bằng đáy).

Trên đây là tổng hợp kiến ​​thức về Lăng trụ tam giác đều, lăng trụ tam giác đều, lăng trụ tứ giác đều và cách tính thể tích khối lăng trụ đều. Nếu bạn có bất kỳ câu hỏi hoặc thắc mắc nào, vui lòng để lại nhận xét bên dưới. Cảm ơn bạn ^^ Nếu thấy hay thì hãy chia sẻ nhé <3

Xem chi tiết bài giảng của thầy Trần Linh:

(Nguồn: www.youtube.com)