Các phương pháp chứng minh tứ giác nội tiếp

Chứng minh “tứ giác nội tiếp” trong câu hỏi toán 9 là dạng câu hỏi phổ biến và thường xuyên gặp trong các kì thi quan trọng. Để giúp học sinh nắm chắc kiến ​​thức và kỹ năng, thầy Nguyễn Quyết Thắng, giáo viên môn Toán của hệ thống giáo dục hocmai đã có một bài giảng giúp các em lấy trọn điểm phần đó. Hãy cùng tìm hiểu!

Bạn Đang Xem: Các phương pháp chứng minh tứ giác nội tiếp

Để chứng minh một tứ giác nội tiếp ta cần chứng minh 4 đỉnh của tứ giác đó cùng nằm trên một đường tròn. Loại bài tập này sẽ có nhiều cấp độ để thử thách học sinh trung cấp và cao cấp trong chương trình Toán lớp 9. Trong quá trình học và theo dõi trên lớp, người học phải tập trung cao độ, ghi chép bài tốt thì mới có thể học hiệu quả.

Trích dẫn:

Cách chứng minh 2 tam giác đồng dạng

Cách xác định tâm đường tròn ngoại tiếp

Một số kiến ​​thức quan trọng về tứ giác nội tiếp

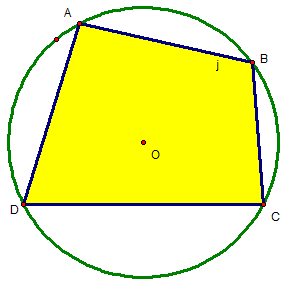
• • Định nghĩa: Tứ giác có bốn đỉnh nằm trên cùng một đường tròn gọi là tứ giác nội tiếp.
  • Lý thuyết: Trong một tứ giác nội tiếp, tổng số đo hai góc đối đỉnh bằng 180 độ.
  • Định lý ngược: Một tứ giác nội tiếp trong một đường tròn nếu tổng hai góc đối diện của nó bằng 180 độ.
  • Ngoài ra, ta có một số kết luận:– Hai góc nội tiếp cùng chắn một cung thì bằng nhau. – Góc nội tiếp bằng nửa góc ở tâm cùng chắn một dây cung. – Góc gồm tiếp tuyến và dây cung của góc nội tiếp cùng chắn một dây cung.

  Phương pháp chứng minh tứ giác nội tiếp

  Cách 1: Chứng minh tổng hai góc đối đỉnh bằng 180 độ

  Xem Thêm: Vật Lí 7 | Giải Vật Lí lớp 7 Kết nối tri thức, Chân trời sáng tạo, Cánh

  Phương pháp này bắt nguồn từ định nghĩa tứ giác nội tiếp. Nội dung của phương pháp như sau: “Nếu tổng hai góc đối diện của tứ giác abcd bằng 180 độ thì tứ giác đó là tứ giác nội tiếp”

  Xem Thêm : Người cách mạng phải học suốt đời căn dặn ai?

  

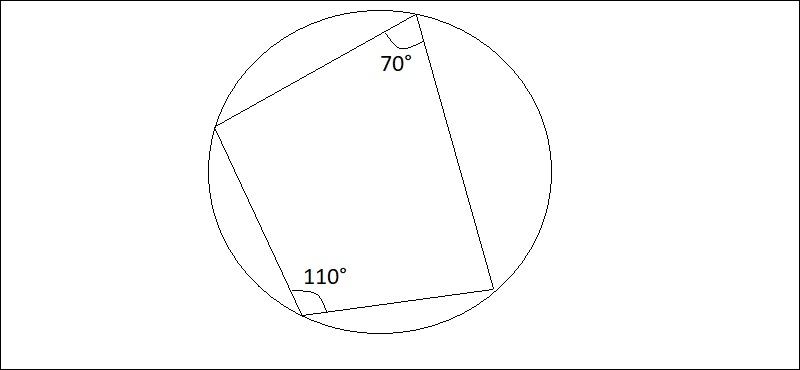
  Kết quả của nội dung này là:

  Cho tứ giác abcd:

  • Nếu bad = bcd = 90 độ thì tứ giác abcd nội tiếp đường tròn tâm o, đường kính bd
  • Nếu tổng hai góc kề bù ead = bcd thì tứ giác abcd nội tiếp

  Cách 2: Chứng minh góc ngoài của một đỉnh bằng góc trong của một đỉnh thuộc đường chéo của một tứ giác

  Với phương pháp này, học sinh phải chú ý nhìn đúng hình, đúng góc độ, nếu không sẽ bị chứng minh là sai nhưng kết quả lại đúng và ảnh hưởng đến câu tiếp theo. Cụ thể, khi bài toán là tứ giác abcd và chứng minh được góc ngoài tại đỉnh a bằng góc c của tứ giác (góc a ngược với góc c) thì có thể kết luận tứ giác abcd là tứ giác nội tiếp.

  

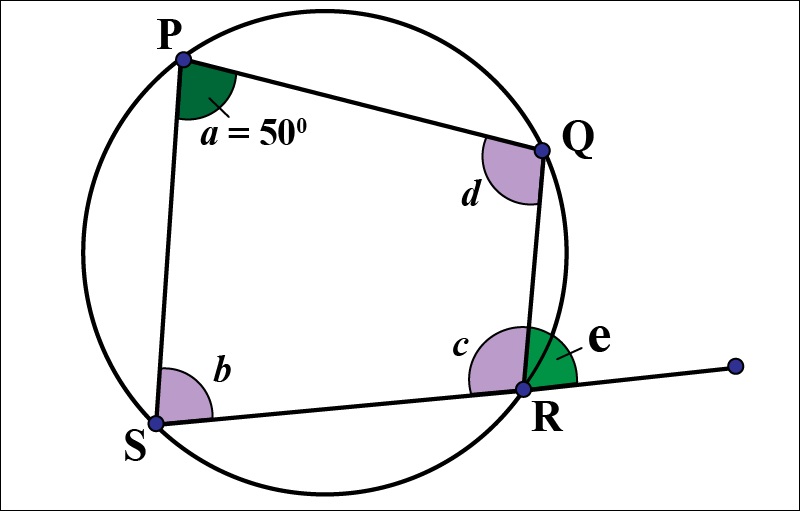
  Cách 3: Chứng minh hai đỉnh kề cùng một phía, nhìn cùng một phía hai góc bằng nhau và bằng 90 độ

  Xem Thêm: Lá mía là gì? Lá mía bò là bộ phận nào?

  Phương pháp này hiệu quả khi bài toán là tứ giác abcd và dữ liệu cho thấy dac = dbc = 90 độ. Từ đó HS rút ra kết luận: Tứ giác abcd nội tiếp đường tròn.

  Cách 4: Chứng minh 4 đỉnh của một tứ giác cách đều một điểm cho trước

  Nếu cho một đường tròn tâm o bán kính r thì khoảng cách từ một điểm bất kỳ trên đường tròn đến tâm chính bằng bán kính. Theo cách dạy của giáo viên, theo tính chất này, học sinh dễ dàng chứng minh được một tứ giác nội tiếp một đường tròn.

  

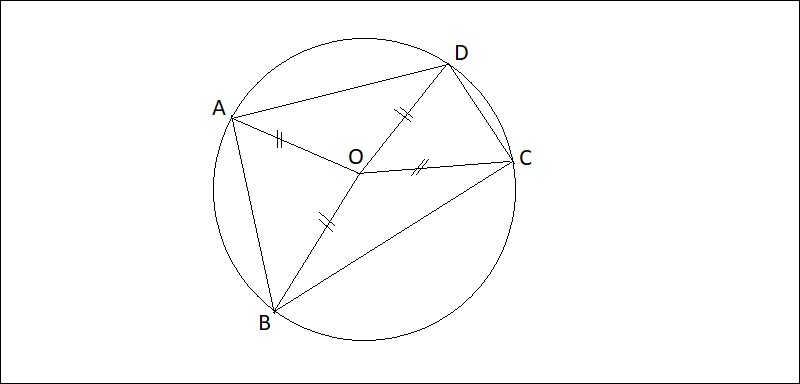
  Ví dụ: Cho điểm o cố định và tứ giác abcd.

  Xem Thêm : Soạn bài Người kể chuyện trong văn bản tự sự

  Nếu học sinh chứng minh được bốn điểm a, b, c, d cách đều điểm o và có khoảng cách bằng r, tức là oa = ob = oc = od = r thì điểm o là tâm của đường tròn đi qua bốn điểm. A B C D. Nói cách khác, tứ giác abcd nội tiếp trong đường tròn tâm o bán kính r.

  Cách 5: Nếu tổng hai cặp góc đối diện của một tứ giác thì tứ giác đó nội tiếp trong một đường tròn

  Với phương pháp này, chỉ cần học sinh chứng minh được tổng hai góc đối đỉnh bằng 180 độ là có thể kết luận tứ giác nội tiếp đường tròn.

  Xem Thêm: Top 9 mẫu phân tích bài thơ Ánh trăng siêu hay

  Ví dụ: Cho tứ giác abcd nội tiếp

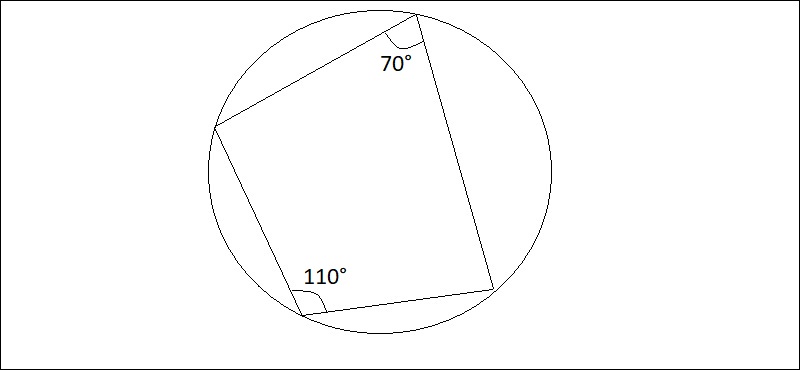
  Cho tứ giác abcd nội tiếp ⇔ góc a + góc c = góc b + góc d. Trường hợp đặc biệt tổng các góc đối đỉnh bằng 180 độ ta ​​được kết quả của cách 1.

  

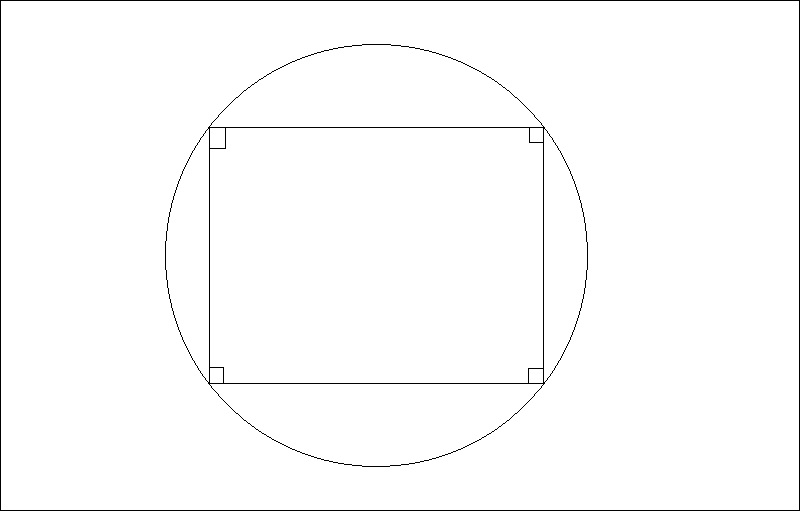
  Cách 6: Chứng minh một tứ giác là tứ giác đặc biệt

  Hãy vận dụng phương pháp này để chứng minh tứ giác đã cho là hình vuông, hình chữ nhật, hình thoi, hình bình hành,… rồi suy ra tứ giác đã cho là tứ giác nội tiếp.

  

  Một số lưu ý khi chứng minh tứ giác nội tiếp

  • Học sinh nên vẽ hình rõ ràng, dễ hiểu, tránh vẽ trong một số trường hợp đặc biệt.
  • Các ký hiệu cho các góc và đường thẳng bằng nhau phải được đánh dấu rõ ràng.
  • Bám sát các giả thuyết và tìm hiểu kiến ​​thức để kiểm tra chúng một cách hiệu quả.
  • Nhu cầu của vấn đề cũng có thể là hướng gợi ý để giải quyết vấn đề.
  • Đừng sao lưu nó với những gì bạn cần chứng minh.

  Trên đây là 4 phương pháp và lưu ý giúp học sinh chứng minh tứ giác nội tiếp đơn giản và hiệu quả hơn. Các em chú ý nghe giảng, ghi chép kỹ lưỡng để nắm chắc kiến ​​thức vận dụng vào bài tập. Đồng thời, phụ huynh muốn giúp con ôn luyện môn toán cuối năm, ôn thi vào lớp 10 THCS hiệu quả có thể đăng ký các khóa học online cho con tại nhà, tiết kiệm thời gian du học.

  Hệ thống giáo dục hocmai tự hào là nền tảng học trực tuyến số 1 dành cho học sinh cấp 3 tại Việt Nam và hiện đang triển khai chương trình hay 2020-2021 nhằm giúp học sinh trên cả nước tiếp cận với nguồn tài liệu, bài giảng chất lượng từ các giáo viên có nhiều năm kinh nghiệm trong nghề giáo viên. Hãy tham gia chương trình ngay hôm nay để tự tin và học tập đột phá!