Biểu diễn hình học của số phức là gì? Công thức và cách dạng bài tập

Thế nào là biểu diễn hình học của số phức? Công thức và bài tập

1) Định nghĩa biểu diễn hình học phức hợp

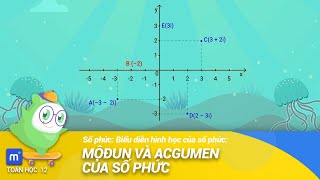
Mỗi số phức $z=x+yi$ được biểu diễn bằng một điểm $m\left( x;y \right)$, sau đó $\overrightarrow{om}=\left( x;y Right)$ trong mặt phẳng phức. Chúng tôi viết $m\left( x+yi \right)$ hoặc $m\left( z \right)$.

Bạn Đang Xem: Biểu diễn hình học của số phức là gì? Công thức và cách dạng bài tập

Sau đó $\left| z \right|=\left| \overrightarrow{om} \right|=\sqrt{{{x}^{2}}+{{y}^{ 2}}}$

Nếu điểm $m\left( {{z}_{1}} \right)$ là điểm biểu diễn số phức ${{z}_{1}}$ và điểm $n left( { {z}_{2}} \right)$ là một điểm đại diện cho số nhiều ${{z}_{2}}$ thì ${{z}_{1}}-{{z} _ {2 }} =\overrightarrow{om}-\overrightarrow{on}=\overrightarrow{nm},{{z}_{1}}+{{z}_{2}}=\overrightarrow { om} + overrightarrow{on}$.

2) Phương pháp giải quyết vấn đề

@Câu 1: Tìm tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $f\left( z;\overline{z} \right)=g\ left ( z ;\overline{z} \right)$ hoặc $f\left( z;\overline{z} \right)$ là số thực hoặc $f\left( z;\ gạch đầu dòng {z} \right)$ là số ảo

Phương pháp giải: sử dụng $z=x+yi\left( x;y\in \mathbb{r} \right)\rightarrow \overline{z}=x-yi$ để thay thế công thức biểu thức ban đầu, các phép biến đổi và kết luận.

Mối quan hệ giữa $x$ và $y$

Tập hợp điểm cuối $m\left( x;y \right)$

Xem Thêm: Văn mẫu lớp 10: Kể lại một kỉ niệm sâu sắc về mẹ (Dàn ý & 21 mẫu) Những bài văn mẫu lớp 10 hay nhất

○ $ax+by+c=0$

Đó là một đường thẳng $ax+by+c=0$

Xem Thêm : Top 14 bài nghị luận về lòng dũng cảm siêu hay

○ $\left[ \begin{array} {} {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2 }}={{r}^{2}} \\ {} {{x}^{2}}+{{y}^{2}}-2ax-2by+c=0 \\ end{array} \right.$

là một hình tròn $\left( c \right)$, tâm là $i\left( a;b \right)$, bán kính là $r=\sqrt{{{a} ^{2 } }+{{b}^{2}}-c}$

○ $\left[ \begin{array} {} {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2 }}\le {{r}^{2}} \\ {} {{x}^{2}}+{{y}^{2}}-2ax-2by+c\le 0 \ \end{array} \right.$

là một hình tròn $\left( c \right)$, tâm là $i\left( a;b \right)$, bán kính là $r=\sqrt{{{a} ^{2 } }+{{b}^{2}}-c}$ (bao gồm cả hình tròn và điểm bên trong).

○ $r_{1}^{2}\le {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2} }\le r_{2}^{2}$

Nó bao gồm hai vòng tròn đồng tâm $i\left( a;b \right)$ và bán kính ${{r}_{1}}$ và ${{r}_ {2}}$

Xem Thêm: Ý nghĩa hình xăm Nhật cổ, 60 mẫu hình xăm Nhật cổ đẹp

○ $y=a{{x}^{2}}+bx+c$

là một parabol $\left( p \right)$ có đỉnh $i\left( -\frac{b}{2a};-\frac{\delta }{4a} phải)$

○ $\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b} ^{2}}}=1$ với $\left\{ \begin{array} {} m{{f}_{1}}+m{{f}_{2}}=2a \ \ {} {{f}_{1}}{{f}_{2}}=2c<2a \\ \end{array} \right.$

là hình elip có trục chính $2a$, trục nhỏ $2b$, tiêu cự ${{f}_{1}}{{f}_{2}}=2c=2\sqrt{{{ a }^{2}}+{{b}^{2}}};\left( a>b>0 \right)$

Một số trường hợp đặc biệt:

þ Tìm tập hợp các điểm biểu diễn số phức $z$ sao cho $\left| z-\left( a+bi \right) \right|=\left| z-\left ( c+di \right) \right|$

Xem Thêm : Sơ đồ tư duy bài Việt Bắc đầy đủ nhất ✔

gọi $m\left( z \right);\,\,a\left( a;b \right);\,\,b\left( c;d right)$ là điểm biểu diễn các số phức $z;\,\,a+bi$ và $c+di$.

Sau đó $\left| z-\left( a+bi \right) \right|=\left| z-\left( c+di \right) \right|\ leftrightarrow ma=mb\rightarrow $ nghĩa là tập điểm phức $z$ trực giao với $ab$.

þ Tìm tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $\left| z-\left( a+bi \right) \right|=r\left( r>0 \ phải)$

Xem Thêm: Toán 7 Bài 7 Kết nối tri thức, Cánh diều, Chân trời sáng tạo

Gọi $m\left( z \right);\,\,i\left( a;b \right)$ lần lượt biểu diễn các điểm của phức $z$ và $a + bi $

Khi đó $\left| z-\left( a+bi \right) \right|=r\leftrightarrow mi=r\rightarrow $ đại diện cho tập điểm phức $z$ là $i left( a ; đường tròn tâm b \right)$ bán kính $r$.

þ Bài toán 2: Tìm tập hợp các điểm biểu diễn phức $w$, biết rằng $w={{z}_{1}}.z+{{z}_{2} }$ và phức $z$ thỏa mãn $\left| z-a-bi \right|=r$

Ta có: $z=\frac{w-{{z}_{2}}}{{{z}_{1}}}$ suy ra $\left| z-a-bi \right| =r\leftrightarrow \left| \frac{w-{{z}_{2}}}{{{z}_{1}}}-a-bi \right|=r\leftrightarrow left| w-{{z}_{2}}-{{z}_{1}}\left( a+bi \right) \right|=r\left| {{z}_ {1}}\right|$

Tập hợp các điểm đại diện cho $w$ dưới dạng hình tròn {{z}_{1}} \right|$ có bán kính $r\left|,

Tổng quát: Tìm tập hợp các điểm biểu diễn các số phức $w$, biết $w={{z}_{1}}.z+{{z}_{2}}$ và số phức $z$ thỏa mãn $\left| z.{{z}_{0}}-a-bi \right|=r$ (thêm phần tử ${{z}_{0}}$)

Ta có: $z=\frac{w-{{z}_{2}}}{{{z}_{1}}}$ suy ra $\left| z.{{z}_ {0}}-a-bi \right|=r\leftrightarrow \left| {{z}_{0}} \right|\left| \frac{w-{{z}_{ 2}}}{{{z}_{1}}}-\frac{a+bi}{{{z}_{0}}} \right |=r\leftrightarrow \left| w- {{z}_{2}}-\frac{{{z}_{1}}\left( a+bi \right)}{{{z}_{0}}} \right| =\frac{r\left| {{z}_{1}} \right|}{\left| {{z}_{0}} \right|}$

Tập hợp các điểm đại diện cho $w$ dưới dạng hình tròn {{z}_{1}} \right|}{\left| {{z}_{ bán kính $\frac{r\left | 0}} \right|}$.