Giải bài 23,24,25 ,26,27,28 ,29,30 trang 66,67 SGK Toán 7 tập 2

Đọc 4 tính chất về ba đường trung tuyến của một tam giác: Giải bài 23,24 trang 66; bài 25,26,27,28,29,30 trang 67 sgk toán 7 tập 2 chương 3 hình học.

Bạn Đang Xem: Giải bài 23,24,25 ,26,27,28 ,29,30 trang 66,67 SGK Toán 7 tập 2

23. Gọi g là trọng tâm của Δdef và đường trung trực là dh. Khẳng định nào sau đây là đúng?

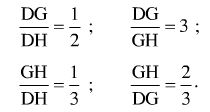
g là trọng tâm và trung tuyến dh của Δdef. Phát biểu đúng là:

24. cho hình ảnh hồ sơ. Điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a) mg = … ông ; gr = … ông; gr = … mg

b) ns = ..ng; ns = …gs; ng = gs

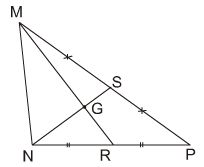
Hình vẽ cho chúng ta biết hai đường trung trực mr và ns cắt nhau tại g nên g là trọng tâm của tam giác. Vì vậy, chúng tôi nhập các số như sau:

Bài 25, trang 67. Biết: Trong hình vuông, trung tuyến của cạnh bằng nửa cạnh huyền. Vui lòng giải quyết các vấn đề sau:

Vì Δvuông abc có hai cạnh ab = 3cm, ac = 4cm. Tính khoảng cách từ đỉnh a đến trọng tâm g của abc.

Giải thích:Δabc vuông tại a =>; bc2 = ab2 + ac2

bc2 = 32 + 42

bc2 = 25

bc = 5

Gọi m là trung điểm của bc => am là trung trực của nửa cạnh huyền nên am = 1/2 bc

Vì g là trọng tâm của abc nên:

26. Chứng minh định lý: Trong một mặt phẳng cân, đường trung trực của hai cạnh bằng nhau.

Giả sử abc cân tại a, có hai trung tuyến bm và cn, ta chứng minh bm = cn

Ta có an = nb = ab/2 (thuộc tính của đường giữa)

am = mc = ac/2 (thuộc tính đường giữa)

Vì ∆ abc cân tại a=> ab = ac nên am = an

Xem bam ;Δ có thể có:

am = an (cm)

Xem Thêm: Cho biết những điểm giống nhau và khác nhau giữa các hình thức

Góc bình thường

ab = ac(Δabc cân)

Có nên suy ra bam = can (c-g-c)

=> bm = cn (2 cạnh tương ứng)

bài 27.Chứng minh nghịch đảo của định lý trên: Nếu Δ có hai trung tuyến bằng nhau thì cân.

Giả sử abc có hai trung tuyến be và cf cắt nhau tại g

=>g là trọng tâm của

Xem Thêm : Tranh tô màu Robot cho bé

=>gb = 2/3 đúng; GC = 2/3 cf

tức là be = cf (giả sử) nên gb = gc

=> Δgbc cân gcb = gbc tại g => gt;

Xem xét bgf và cge với:

gb = gc (cmt)

Góc bgf = góc cge (2 góc đối đỉnh)

ge=gf

⇒ bgf = cge (c-g-c)

⇒ bf = ce (tương ứng 2 vế)

Xét Δfbc và Δecb trong đó bf = ce (cmt) cạnh bc chung be = cf (gt)

⇒ Δfbc = Δecb(c-c-c) ⇒ góc b = góc c vì Δabc có góc b = góc c ⇒ Δabc là Δ cân tại a. (2 góc ở đáy bằng nhau)

Sau 28.Vì Δdef bằng d và trung vị di

a) Chứng minh rằng dei = dfi

b) Góc die và dif là gì?

c) Biết de = df = 13cm, ef = 10cm, tính độ dài đường trung tuyến.

Giải:a) ∆dei = ∆dfi có:

di là mặt chung

de = df (số dư nợ)

tức là = nếu (di là median.line)

Xem Thêm: Cảm nhận về nhân vật Lão Hạc (30 mẫu) SIÊU HAY

=> Δdei = Δdfi (c.c.c)

b) Vì Δdei = Δdfi =>cái chết=sự khác biệt

die + dif= 1800 (liền kề)

do diem = dif = 900

c) i là trung điểm của ef nên ie = if = 5cm

Δdei bình phương tại i => di2 = de2 – ei2 (định lý pytagogue)

=> di2 = 132 – 52 = 144

=> di = 12

Bài 29, trang 67. Gọi g là trọng tâm của Δmọi abc. Bằng chứng:

ga =gb = gc

Cho m, n, e là giao điểm của ag, bg, cg và bc, ca, ab.

Vì g là trọng tâm của abc

Vì Δabc đều nên ba giá trị trung tuyến của các đường thẳng ứng với ba cạnh bc, ca, ab đều bằng nhau

=>am = bn = ce (2)

Từ (1), (2) => ga = gb = gc

Bài 30 trang 67 Toán 7: Gọi g là trọng tâm của Δabc. Lấy điểm g’ trên tia ag sao cho g là trung điểm của ag’

a) So sánh biên của Δbgg’ với trung tuyến của Δabc

b) So sánh trung tuyến của Δbgg’ với các cạnh của Δabc.

Xem Thêm : Khối H gồm những môn nào? Các trường đại học khối H

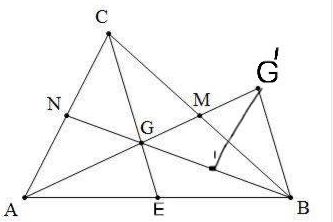
a) So sánh cạnh của bgg’ với trung tuyến của abc bg cắt nhau tại n ac

cg cắt ab tại e

g là trọng tâm của abc

=>ga = 2/3 sáng

ga = gg’ (g là trung điểm của ag’)

gg’ = 2/3 giờ sáng

Vì g là trọng tâm của ∆abc => gb = 2/3 tỷ

Ngược lại: gm = 1/2 ag (g là trọng tâm)

Xem Thêm: Soạn bài Củng cố, mở rộng bài 8 Kết nối tri thức

ag = gg’ (gt)

gm = 1/2 gam’

m là trung điểm gg’

Vậy gmc = g’mb vì:

gram=mg’

mb = mc

∠gmc = g’mb

=>bg’ = cg

trong đó cg = 2/3 ce (g là trọng tâm abc)

=> bg’ = 2/3 ce

Vậy mỗi cạnh của bgg’ bằng 2/3 trung tuyến của Δabc

b) So sánh trung tuyến của ∆bgg’ với cạnh ∆abc

Ta có: bm là đường trung bình của bgg’

với m là trung điểm của bc nên bm = 1/2 bc

Vì ig = 1/2 bg (i là trung điểm của bg)

gn = 1/2 bg (g là trọng tâm)

=>ig = gn

Do đó ∆igg’ = ∆nga (cgc) => ig’ = a => ig’ = ac/2

– Gọi k là trung điểm bg => gk là trung tuyến ∆bgg’

Vì ge = 1/2 gc (g là trọng tâm abc)

=>ge = 1/2 bg

với k là trung điểm bg’ => kg’ = eg

Vì gmc = g’bm (đã chứng minh ở trên)

=> ∠gcm = ∠g’bm (góc đáy nội tiếp lại)

=>ce // bg’ => age = ag’b(isotope)

Do đó ∆age = ∆gg’k (cgc) => ae = gk

ae = 1/2 ab nên gk = 1/2 ab

Vậy mỗi đường trung tuyến bgg’ bằng một nửa các cạnh song song của abc