Giải bài 36, 37, 38, 39 trang 82, 83 SGK Toán lớp 9 tập 2

bài 36 trang 82 sgk toán 9 tập 2

Bạn Đang Xem: Giải bài 36, 37, 38, 39 trang 82, 83 SGK Toán lớp 9 tập 2

Sau 36. Cho đường tròn \((o)\) và hai xâu \(ab\), \(ac\). Gọi \(m, n\) lần lượt là trung điểm của các cung \(ab\) và \(ac\). Dòng \(mn\) cắt chuỗi \(ab\) tại \(e\) và cắt dòng \(ac\) tại \(h\). Chứng minh rằng tam giác \(aeh\) là tam giác cân.

Xem Thêm: Các đới khí hậu trên Trái Đất là gì? – Dự báo thời tiết

Hướng dẫn giải quyết:

Ta có: \(\widehat {ahm}\)= \(\frac{sđ\overparen{am}+sđ\overparen{nc}}{2}\) (1 )

\(\widehat {aen}\)= \(\frac{sđ\overparen{mb}+sđ\overparen{an}}{2}\) (2)

p>

(vì \widehat {ahm}\) và \(\widehat {aen}\) là các góc cố định bởi các đỉnh bên trong đường tròn.

Giả định:

\(\overparen{am}=\overparen{mb} (3)\)

\(\overparen{nc}=\overparen{an} (4)\)

Được suy ra từ (1), (2), (3), (4) \(\widehat {ahm}\)= \(\widehat {aen}\) Do đó ( ∆ aeh\) là tam giác cân.

Bài 37 Trang 82 SGK Toán 9 Tập 2

Sau 37. Cho đường tròn \((o)\) và hai xâu \(ab\), \(ac\) là tương đương. Lấy một điểm \(m\) trên cung nhỏ \(ac\). Gọi \(s\) là giao điểm của \(am\) và \(bc\). Chứng minh: \(\widehat {asc}\)=\(\widehat {mca}\)

Xem Thêm: Các đới khí hậu trên Trái Đất là gì? – Dự báo thời tiết

Hướng dẫn giải quyết:

Ta có: \(\widehat {asc}\)= \(\frac{sđ\overparen{ab}+sđ\overparen{mc}}{2}\) (1 )

(\(\widehat {asc}\) là góc có đỉnh nằm ngoài đường tròn \((o)\))

Xem Thêm : Giờ Tỵ là mấy giờ? Người sinh giờ Tỵ vận mệnh tốt hay xấu?

Và \(\widehat {mca}\)=\(\frac{sd\overparen{am}}{2}\) (2)

(Góc cắt nội tiếp \(\overparen{am}\))

Giả định:

\(ab = ac =>\)\(\overparen{ab}=\overparen{ac}\) (3)

Từ (1), (2), (3): \(\overparen{ab}-\overparen{mc}=\overparen{ac}-\overparen{mc}= overparen {am}\)

Từ đó \(\widehat {asc}=\widehat {mca}\).

Bài 38 Trang 82 SGK Toán 9 Tập 2

Sau 38. Trên một đường tròn, lấy ba cung liên tiếp \(ac, cd, db\) như thế này

\(sd\overparen{ac}\)=\(sđ\overparen{cd}\)=\(sđ\overparen{db}\)=\(60^ ) 0\). Hai đường thẳng \(ac\) và \(bd\) cắt nhau tại \(e\). Hai tiếp tuyến của đường tròn cắt nhau tại \(t\) tại \(b\) và \(c\). Bằng chứng:

Xem Thêm: Văn mẫu lớp 12: Nghị luận về tầm quan trọng của việc học Dàn ý & 13 bài tầm quan trọng của việc học

a) \(\widehat {aeb}=\widehat {btc}\);

b) \(cd\) là tia phân giác của \(\widehat{btc}\)

Xem Thêm: Các đới khí hậu trên Trái Đất là gì? – Dự báo thời tiết

Hướng dẫn giải quyết:

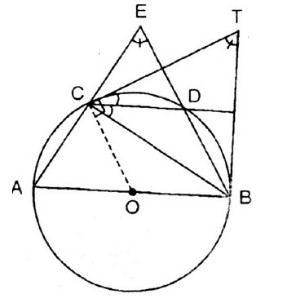
a) Ta có \(\widehat{aeb}\) là góc có đỉnh nằm ngoài đường tròn nên:

\(\widehat{aeb}\)=\(\frac{sd\overparen{ab}-sđ\overparen{cd}}{2}\)=\({ {{{180}^0} – {{60}^0}} \ trên 2} = {60^0}\)

Và \(\widehat{btc}\) cũng là góc có đỉnh nằm ngoài đường tròn (hai cạnh tiếp xúc với đường tròn) nên:

Xem Thêm : Dàn ý cảm nhận về nhân vật Phương Định trong Những ngôi sao xa

\(\widehat{btc}\)=\(\frac{\widehat {bac}-\widehat {bdc}}{2}\)=\({{( {{180}^0} + {{60}^0}) – ({{60}^0} + {{60}^0})} \ trên 2} = {60^0}\)

Vậy \(\widehat {aeb} =\widehat {btc}\)

b) \(\widehat {dct} \) là góc tạo bởi tiếp tuyến và dây cung nên:

\(\widehat {dct}=\frac{sđ\overparen{cd}}{2}\)

\(\widehat {dcb}\) là góc nội tiếp trên

Xem Thêm: Cảm Nghĩ Bài Thơ Bánh Trôi Nước – Nên Tham Khảo

\(\widehat {dcb}=\frac{sđ\overparen{db}}{2}={{{{60}^0}} \trên 2} = {30^0} \)

Vậy \(\widehat {dct}=\widehat {dcb}\) hay \(cd\) là tia phân giác của \(\widehat {bct} \)

Bài 39 Trang 83 SGK Toán 9 Tập 2

bài 39. Với \(ab\) và \(cd\) là hai đường kính vuông góc của đường tròn \((o)\). Lấy một điểm \(m\) trên cung nhỏ \(bd\). Tiếp tuyến tại \(m\) cắt tia \(ab\) tại \(e\) và đoạn thẳng \(cm\) cắt \(ab\) tại ( s ).Proof\(es = em\).

Xem Thêm: Các đới khí hậu trên Trái Đất là gì? – Dự báo thời tiết

Hướng dẫn giải quyết:

Ta có \(\widehat{mse}\) = \(\frac{sđ\overparen{ca}+sđ\overparen{bm}}{2}\) (1)

(vì \(\widehat{mse}\) là góc của đỉnh s bên trong đường tròn (o))

\(\widehat{cme}\) = \(\frac{sd\overparen{cm}}{2}\)= \(\frac{sđ\overparen{ cb}+sđ\overparen{bm}}{2}\) (2)

(\(\widehat{cme}\) là góc tạo bởi tiếp tuyến và dây cung).

Giả sử \(\overparen{ca}=\overparen{cb}\) (3)

Từ (1), (2), (3) ta có: \(\widehat{mse}\) = \(\widehat{cme}\) Từ đó \(Δesm ) là tam giác cân và \(es = em\)

giaibaitap.me