Giải bài 4, 5, 6 trang 36, 37, 38 SGK Toán 9 tập 2 – Giaibaitap.me

Bài 4 Trang 36 SGK Toán 9 Tập 2

Bạn Đang Xem: Giải bài 4, 5, 6 trang 36, 37, 38 SGK Toán 9 tập 2 – Giaibaitap.me

Bản phát hành 4. Đối với hai hàm: \(y = {3 \over 2}{x^2},y = – {3 \over 2}{x^2}\). Điền vào bảng dưới đây, rồi vẽ hai hình trên cùng một mặt phẳng tọa độ.

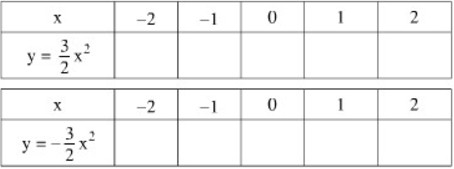
Nhận xét tính đối xứng của hai hình qua trục ox.

Giải pháp thay thế:

Tính và điền vào chỗ trống để được bảng sau:

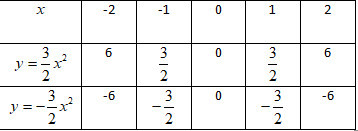
Biểu đồ:

Nhận xét: Đồ thị của hai hàm số đối xứng nhau qua trục ox.

Bài 5 Trang 37 SGK Toán 9 Tập 2

Xem Thêm: Văn mẫu lớp 12: Phân tích diễn biến tâm trạng Mị trong đêm tình mùa xuân (19 Mẫu) Mị trong đêm tình mùa xuân

Bản phát hành 5. Ba chức năng:

\(y = {1 \ trên 2}{x^2};y = {x^2};y = 2{x^2}\)

a) Vẽ ba hàm số trên cùng một mặt phẳng tọa độ.

Xem Thêm : TANG LỄ NSƯT MINH PHỤNG: PHẦN 1

b) Tìm ba điểm \(a, b, c\) \(x = -1,5\) có cùng tọa độ theo thứ tự của chúng trên ba đồ thị. Xác định tọa độ tương ứng của chúng.

c) Tìm ba điểm \(a’, b’, c’\) có cùng tọa độ\(x = 1.5\) theo thứ tự trên ba đồ thị. Kiểm tra tính đối xứng của a và a’, b và b’, c và c’.

d) Với mỗi hàm số trên, hãy tìm giá trị của x sao cho giá trị của hàm số là nhỏ nhất.

Giải pháp thay thế:

a) Bản vẽ

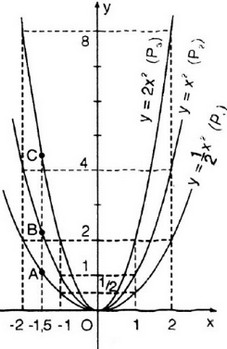
b) Tọa độ của \({y_a},{y_b},{y_c}\) và điểm \(a,b,c\) có cùng tọa độ lần lượt là \(x = ) -1,5\). Chúng tôi có:

Xem Thêm: Hình ảnh con trâu đẹp

\(\eqalign{ & {y_a} = {1 \ trên 2}{( – 1,5)^2} = {1 \ trên 2}.2,25 = 1,125 \cr & {y_b} = {( – 1,5)^2} = 2,25 \cr & {y_c} = 2{( – 1,5)^2} = 2,2,25 = 4,5 \cr} \)

c) gọi \({y_{a’}},{y_{b’}},{y_{c’}}\) tọa độ điểm\(a))’ , b ‘, c’\) có cùng tọa độ \(x = 1,5\). Chúng tôi có:

\(\eqalign{ & {y_{a’}} = {1 \ trên 2}{(1,5)^2} = {1 \ trên 2}.2,25 = 1,125 \cr & {y_{b’}} = {(1,5)^2} = 2,25 \cr & {y_{c’}} = 2{(1,5)^2} = 2,2,25 = 4,5 \cr} \)

Kiểm tra tính đối xứng: a và a’, b và b’, c và c’ đối xứng qua trục tung oy.

d) Với mỗi hàm đã cho, ta có các hệ số \(a > 0\) nên o là điểm thấp nhất của đồ thị.

Vậy \(x = 0\) thì hàm số đạt giá trị nhỏ nhất.

Bài 6 Trang 38 SGK Toán 9 Tập 2

Xem Thêm : Lọc dữ liệu trong dải ô hoặc bảng

Sau 6. Đối với hàm \(y = f(x) = {x^2}\).

a) Vẽ đồ thị của hàm.

b) Giá trị tính toán\(f(-8); f(-1,3); f(-0,75); f(1,5)\).

Xem Thêm: Hãy nêu nguyên nhân thắng lợi và ý nghĩa lịch sử của phong trào

c) Sử dụng ước tính biểu đồ \({(0.5)^2};{( – 1.5)^2};{(2,5)^2}\) .

d) Sử dụng đồ thị để ước tính vị trí của một điểm trên trục hoành biểu thị số \(\sqrt{3}; \sqrt{7}\).

Giải pháp thay thế:

a) Vẽ đồ thị hàm số y = x2.

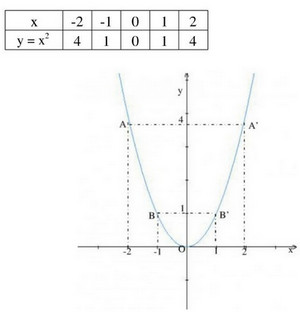
b) Ta có \(y = f(x) = {x^2}\) nên

\(\eqalign{ & f\left( { – 8} \right){\rm{ }} = {\rm{ }}{\left( { – 8} right)^2} = {\rm{ }}64;{\rm{ }}f\left( { – 1.3} \right){\rm{ }} = {\rm { } }{\left( { – 1,3} \right)^2} = {\rm{ }}1,69;{\rm{ }} \cr & f\left( { – 0,75} \right){\rm{ }} = {\rm{ }}{\left( { – 0,75} \right)^2} = {\rm{ } } }0,5625; \cr & {\rm{ }}f\left( {1.5} \right){\rm{ }} = {\rm{ }}1,{5 ^2} = {\rm{ } }2,25 \cr} \)

c) Theo đồ thị ta có:

\(\eqalign{ & {(0,5)^2} \khoảng 0,25 \cr & {( – 1,5)^2} \khoảng 2,25 \ cr & {(2 ,5)^2} \khoảng 6,25 \cr} \)

d) Theo đồ thị ta có: Điểm \(\sqrt{3}\) trên trục hoành có tọa độ \(y = {(\sqrt 3 )^2} = 3 ) . Sử dụng \( 1,7\) để lấy điểm đại diện cho \(\sqrt{3}\) trên trục hoành. Tương tự như biểu diễn \(\sqrt{7}\) bao gồm \(2.7\).

giaibaitap.me