Giải bài 1, 2, 3, 4 trang 17 Sách giáo khoa Giải tích 11

Bài 1 Trang 17 SGK Giải tích 11

Bạn Đang Xem: Giải bài 1, 2, 3, 4 trang 17 Sách giáo khoa Giải tích 11

Xác định giá trị của \(x\)\(\left[ { – \pi ;{{3\pi } \over 2}} \right] ) trên đoạn văn sao cho hàm\(y = tanx\) ;

a) Nhận giá trị bằng \(0\);

b) lấy giá trị của \(1\);

c) nhận giá trị dương;

d) Nhận giá trị âm.

Trả lời:

a) Trục hoành giao với đồ thị \(y = tanx\) (tương ứng với \(x \in\) \(\left[ { – \pi ;{{3 ) pi } \trên 2}} \right]\)) tại ba điểm có tọa độ – π; 0; π. Vì vậy, trong đoạn \(\left[ { – \pi ;{{3\pi } \over 2}} \right]\) chỉ có ba giá trị \(x ) sao cho hàm \(y = tanx\) nhận giá trị \(0\), nghĩa là \(x = – π; x = 0 ; x = π\).

b) Đường thẳng \(y = 1\) cắt đồ thị \(y = tanx\) (tương ứng với \(x\in\)\(\left[ {) – \pi ;{{3\pi } \trên 2}} \right]\)) tại tọa độ \({\pi \trên 4};{\pi trên 4} \pm \pi\) . Vì vậy, trong đoạn \(\left[ { – \pi ;{{3\pi } \over 2}} \right]\) chỉ có ba giá trị \(x ) sao cho hàm \(y = tanx\) nhận giá trị \(1\), nghĩa là \(x = – {{3\pi } \trên 4};\, \ , x = {\ pi \vượt 4};\,\,x = {{5\pi } \vượt 4}\).

c) Phần đồ thị phía trên trục hoành \(y = tanx\) (tương ứng với \(x \in\) \(\left[ { – \pi ;{ ) { 3\pi } \ trên 2}} \right]\)) theo tọa độ trong khoảng \(\left( { – \pi ; – { pi \trên 2}} \right )\); \(\left( {0;{\pi \trên 2}} \right)\); \(\left( {\pi ;{{ 3\ pi } \ trên 2}} \ phải)\). Vậy trong đoạn \(\left[ { – \pi ;{{3\pi } \over 2}} \right]\), giá trị của \(x\) cho hàm, Số\(y = tanx\) giá trị dương\(x \in \left( { – \pi ; – {\pi \over 2}} \right ) \cup left( {0;{\pi \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right) ).

d) Phần đồ thị bên dưới trục hoành \(y = tanx\) (tương ứng với \(x \in\) \(\left[ { – \pi ;{ ) { 3\pi } \over 2}} \right]\)) bao gồm các điểm trong đồ thị có tọa độ nằm trong khoảng \(\left( { – {\pi over 2 };0 } \right),\left( {{\pi \over 2};\pi } \right)\).Vì vậy, trong đoạn \(\left[ { – \ pi ;{ {3\pi } \over 2}} \right]\), hàm giá trị số \(y = tanx\) của \(x\) nhận giá trị âm là (x \) in \left( { – {\pi \trên 2};0} \phải),\left( { {\pi \trên 2};\pi } \phải)\ )

bài giảng 2 trang 17 sgk giải tích 11

Xem Thêm: 7 Ý nghĩa việc đốt đền của ngô tử văn mới nhất

Đã tìm thấy bộ chức năng:

a) \(y=\frac{1+cosx}{sinx}\) ;

b) \(y=\sqrt{\frac{1+cosx}{1-cosx}}\) ;

c) \(y=tan(x-\frac{\pi }{3})\) ;

Xem Thêm : Bài 1,2,3, 4,5,6 trang 130 SGK Hóa 8: Axit – Bazơ – Muối

d) \( y=cot(x+\frac{\pi }{6})\) .

Người chiến thắng:

Câu a:

Hàm \(y=\frac{1+cosx}{sinx}\) xác định thời điểm \(sinx\neq 0\leftrightarrow x \neq k \pi,k\ in mathbb{z}\)

Vậy tập xác định của hàm là \(d=\mathbb{r} \setminus \left \{ k \pi,k\in \mathbb{z} \right } \)

Câu B:

Hàm \(y=\sqrt{\frac{1+cosx}{1-cosx}}\) xác định thời điểm \(\left\{\bắt đầu{ma trận}\ frac {1+cosx}{1-cosx}\geq 0\\ \\ 1-cosx\neq 0 \end{matrix}\right.\)

\(\leftrightarrow 1-cosx>0(do \ \ 1+cosx\geq 0)\)

\(\leftrightarrow cosx\neq 1 \leftrightarrow x \neq k2 \pi,k\in \mathbb{z}\)

Xem Thêm: Tôi thấy mình đã khôn lớn năm 2021 (dàn ý – 5 mẫu)

Vậy tập xác định của hàm là \(d=\mathbb{r} \setminus \left \{ k 2 \pi,k\in \mathbb{z} \right \ }\)

câu c:

Hàm xác định thời điểm \(cos\left ( x-\frac{\pi }{3} \right )\neq 0\) xác định thời điểm:\(x- frac { \pi }{3}\neq \frac{\pi }{2}+k\pi \leftrightarrow x\neq \frac{5\pi }{6}+k pi (k\in z)\)

Vậy tập xác định của hàm \(d=\mathbb{r} \setminus \left \{ \frac{5\pi }{6}+k \pi ,k in z \right\}\)

Câu d:

Hàm xác định thời điểm \(sin \left ( x+\frac{\pi }{6} \right )\neq 0\) xác định thời điểm \(x+\frac{ pi }{6}\neq k\pi \leftrightarrow x\neq -\frac{\pi }{6}+k\pi,k\in z\)

Vậy tập xác định của hàm là \(d=\mathbb{r} \setminus \left \{ \frac{\pi }{6}+k \pi , k in z \right\}\)

bài 3 trang 17 sgk giải tích 11

Xem Thêm : Lợi ích của việc đi bộ – Bệnh viện Hồng Ngọc

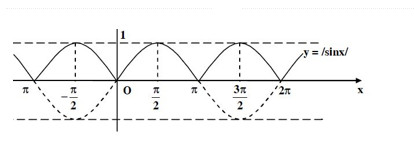
Dựa vào đồ thị của hàm số \(y = sinx\), hãy vẽ đồ thị của hàm số \(y = |sinx|\).

NGƯỜI CHIẾN THẮNG

Chúng tôi có

\(\left| {{\mathop{\rm s}\nolimits} {\rm{inx}}} \right| = \left\{ \ma trận{ { \mathop{\rm s}\nolimits} {\rm{inx}},{\mathop{\rm s}\nolimits} {\rm{inx}} \ge {\ rm{0}} \hfill \cr {\rm{ – sinx}},{\mathop{\rm s}\nolimits} {\rm{inx}} \le 0 \hfill \cr} \Có.\)

Xem Thêm: Tác dụng của ngôi kể thứ nhất?

\(sinx < 0\) \(⇔ x ∈ (π + k2π , 2π + k2π), k ∈ z\) phải đối xứng qua trục \(ox\) trên các các khoảng Đồ thị của hàm số \(y = sinx\) giữ nguyên là đồ thị của hàm số \(y = sinx\) trên đoạn còn lại ta được đồ thị của hàm số \(y = |sinx|\)

Bài 4 Trang 17 SGK Giải tích 11

Chứng minh rằng \(sin2(x + kπ) = sin 2x\) với mọi số nguyên \(k\). Sau đó vẽ đồ thị của hàm \(y = sin2x\).

Trả lời:

do \(sin (t + k2π)\) = \(sint\), \(\forall k \in z\) (chu kỳ của hàm f\( ( t ) = sint)\), từ đó

\(sin(2π + k2π) = sin2x \rightarrow sin2(tx+ kπ) = sin2x\), \(∀k ∈ z\).

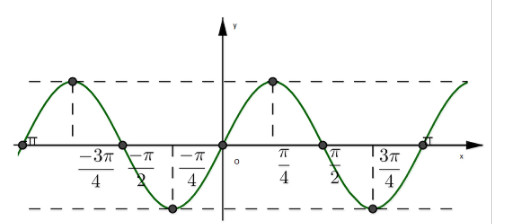
Do tính chất trên nên để vẽ đồ thị hàm \(y = sin2x\) ta chỉ cần vẽ hàm \(π\) (đoạn \) ( left[ { – { \pi over 2};{\pi \over 2}} \right]\) chẳng hạn), sau đó dịch lại độ dài của mỗi đoạn \(π\) dọc theo trục hoành phải và trái.

Với mỗi \(x_0 \in\) \(\left[ { – {\pi \trên 2};{\pi \trên 2}} \right] ) Khi đó \(x = 2x_0\in [-π ; π]\), điểm \(m(x ; y = sinx)\) thuộc đoạn thẳng \((c)\ ) hàm (y = sinx\), \((x ∈ [-π ; π])\) và các điểm thuộc đoạn thẳng\(m'(x_0 ; y_0 = sin2x_0)\) Hàm ((c ‘)\) của \(y = sin2x\), ( \(x ∈\) \(\left[ { – {\pi \trên 2} ; { \pi trên 2}} \right]\)) (h.5).

Chú ý rằng \(x = 2x_0 \rightarrow sinx = sin2x_0\) nên hai điểm \(m’\), \(m\) có cùng tọa độ nhưng bằng nhau của (m’\) là một nửa tọa độ của \(m\). Từ đó, chúng ta có thể thấy rằng \((c’)\) có thể được bắt nguồn từ \((c)\) bằng cách “cuộn” \((c)\) dọc theo trục hoành, như sau:

– Với mỗi \(m(x ; y) ∈ (c)\), gọi \(h\) là hình chiếu đứng của \(m\) dưới trục \(oy) \) và \(m’\) là trung điểm của đoạn thẳng \(hm\) thì \(m’\) \(\left( {{x \over 2} ; y } \right)\) \(∈(c’)\) (khi \(m\) trực tuyến\((c)\) \(m’\) tăng ((c’))\). Trong thực tế, ta chỉ cần đặt điểm đặc biệt của \((c’)\) (chấm \(m’\) vào điểm \((c) \(m\) ) tọa độ \(\ trong \left\{ {0;\,\, \pm {\pi \trên 6};\,\, \ pm { pi \ trên 4};\,\, \pm {\pi \trên 3};\,\, \pm {\pi\trên 2}} right } )).

giaibaitap.me